ОПЫТ ШТЕРНА И ГЕРЛАХА. СПИН ЭЛЕКТРОНА

Немецкие физики О.Штерн и В.Герлах в 1922году поставили опыт, схема которого преведена на рис.2.19.

Через сильно неоднородное вдоль оси Z магнитное поле (N-S) на экран или фотопластинку направляли от источника (И) узкий поток атомов. Атомы (Li, Аg, Н) находились заведомо в невозбужденном состоянии, то есть результирующие орбитальные моменты их электронов были равны нулю, поэтому магнитное поле не должно казалось бы влиять на движение таких атомов. Однако, атомный пучок расщеплялся на две компоненты 1 и 1¹, расположенные симметрично относительно первоначального направления х. Этот результат необъясним с точки зрения классической физики. Получалось, что атомы обладают каким-то еще магнитным моментом (не орбитальным), за счет которого они ориентируются в магнитном поле: либо втягиваются в область более сильного поля, либо выталкиваются в область более слабого.

Рис.2.19

По современным данным электрон является истинно элементарной частицей, то есть, в нем нет составных частей. С классической точки зрения у такого точечного объекта не может быть внутренних состояний. Тем не менее, опыт Штерна и Герлаха невозможно объяснить, если считать, что электрон может находиться лишь в состоянии поступательного движения.

Первым, кто это понял, был В.Паули. В 1924г. он показал, что для объяснения различных свойств атомов, необходимо предположить, что электрон обладает двумя внутренними состояниями, физические характеристики которых не имеют классического аналога.

В 1925г. Дж.Улленбек и С.Гаудсмит высказали смелую гипотезу, согласно которой каждый электрон обладает собственным неуничтожимым механическим моментом 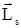, имеющим чисто квантовую природу. Они назвали этот момент спином (spin) и предположили, что два внутренних состояния электрона – это спиновые состояния, характеризующиеся проекциями L_SZ спина на выделенную ось Z. Спин является релятивистской характеристикой и, поэтому, не входит в уравнение Шредингера.

Поскольку электрон – это заряженная частица, то со спином неразрывно связан собственный магнитный момент 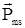, проекция которого на направление магнитного поля, как следует из опыта Штерна и Герлаха, может принимать лишь два значения.

Наглядно это можно представить так, как будто с электроном связана некая “магнитная стрелка”. В отсутствие магнитного поля ее способность к ориентации ни в чем себя не проявляет. Однако при наличии магнитного поля каждый электрон может ориентироваться лишь двумя способами: либо против поля, либо по полю, что и позволяет говорить о двух спиновых состояниях электрона. Согласно общим выводам квантовой механики спин квантуется по закону (аналогия с формулой ( 2.68)):

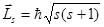, (2.74)

где s – cпиновое квантовое число.

По аналогии с проекцией орбитального момента проекция L_SZ спина тоже квантуется так, что вектор L_S может принимать (2s + 1) ориентаций. Как следует, из опыта Штерна и Герлаха, наблюдается лишь две ориентации, поэтому (2s +1)=2 , поэтому s=1/2, а величина проекции согласно формуле (2.70) определяется выражением

,

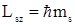где m_S – магнитное спиновое квантовое число, которое может принимать два значения

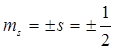. (2.75)

Таким образом, спин электрона полуцелый. Проекция спина на направление магнитного поля (ось Z) может принимать лишь два значения

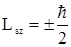. (2.76)

Точная теория спина для электрона следует из уравнения Дирака, которое является релятивистским обобщением уравнения Шредингера (то есть удовлетворяет требованиям теории относительности). Именно из уравнения Дирака следует, что для электрона невозможно значение s = 0.

Своеобразие спина электрона состоит не только в том, что квантовое число s- полуцелое (в отличие от l-целого). Известно, что отношение проекций магнитного и механического орбитальных моментов равно

,

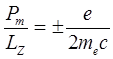тогда как для собственных моментов справедливо отношение

,

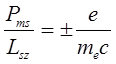то есть, в два раза больше.

Итак, опытные данные привели к необходимости характеризовать каждый электрон добавочной внутренней степенью свободы – магнитным спиновым квантовым числом m_S. Поэтому для полного описания состояния электрона в атоме наряду с квантовыми числами n, l, m_l нужно задавать число m_S.

Таким образом, число различных состояний атома отвечающих данному значению главного квантового числа n равно N_n=2·n². Это обстоятельство важно для понимания закономерностей таблицы элементов Д.И. Менделеева (см. п.2.7.3).