Аксиомы Неймана-Моргенштерна
Аксиома транзитивности. Предпочтения ЛПР являются транзитивными. Например, если субъект предпочитает исход А исходу В, а исход В исходу С, то следовательно, он предпочитает исход А исходу С.
Аксиома безразличия. Если имеется три возможных исхода А, В и С, а ЛПР предпочитает исход А исходу В, а исход В – исходу С, то должна существовать такая вероятность Р, что для ЛПР следующие две альтернативы будут иметь одинаковую ценность:
· получить В наверняка;
· игра, в которой ЛПР выигрывает А с вероятностью Р, либо выигрывает С с вероятностью (1–Р). Значения вероятности могут быть различными, что не имеет принципиального значения. Важно то, что существует определенное значение вероятности Р, при котором для ЛПР будет безразлично: либо принять участие в игре, в которой можно выиграть А или С, либо получить выигрыш В.
Аксиома рациональности. Если ЛПР предложено два лотерейных билета с идентичными призами, то он выберет билет с большей вероятностью выигрыша.
Однако следует заметить, что не все экономисты и статистики разделяют эти аксиомы, но большинство все-таки рассматривает их как вполне разумные допущения, позволяющие строить теорию выбора решения в условиях неопределенности. Также, необходимо отметить, что не все индивидуумы действуют согласно этим аксиомам. Даже если человек согласен со всеми из них, это отнюдь не предполагает, что он не может ошибиться и совершить нерациональное действие. Смысл этих аксиом заключается в том, что они показывают, как люди должны принимать решения для того, чтобы эти решения согласовывались с их предпочтениями, хотя на практике менеджеры не всегда принимают решения, согласующиеся с ними.
Теорема. Каждому результату лотереи можно приписать некоторое число такое, что для любых двух лотерей 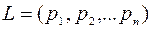 и
и 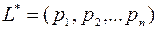 будет верно
будет верно 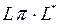 тогда и только тогда, когда
тогда и только тогда, когда 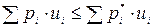 .
.
Число 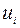 , приписываемое i-му результату, называется его полезностью.
, приписываемое i-му результату, называется его полезностью.
Число 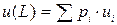 , которое приписывается лотерее L, называется средней ожидаемой полезностью лотереи. Это математическое ожидание этой лотереи.
, которое приписывается лотерее L, называется средней ожидаемой полезностью лотереи. Это математическое ожидание этой лотереи.
Принцип фон Неймана-Моргенштерна:
Индивидуум будет поступать так, чтобы максимизировать значение полезности.
Функция полезности возрастает, причем она линейна, если ЛПР нейтрален к риску, вогнута, если ЛПР несклонен к риску, и выпукла, если ЛПР склонен к риску.
Функция несклонности к риску:
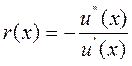
Дата добавления: 2015-08-14; просмотров: 2857;
