Аксиоматический подход к вероятности. Вероятностное пространство. Аксиомы вероятности Колмогорова.
Пусть Ω множество элементарных исходовА– сигма алгебра подмножеств множества Ω называемых событиями, Р – числовая функция, определенная на событиях, называемая вероятностью и обладающая следующими свойствами:
|
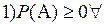 А
А 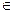 А
А
2) 
3) Если А∙В=0, то Р(А+В)= Р(А)+Р(В) (аддитивность вероятности)
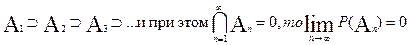
|
Тогда тройка объектов (Ω, А,Р) называется вероятностным пространством.
Аксиомы 3 и 4 можно заменить аксиомой 3* с четной аддитивностью
(сигма аддитивность)

3*) Если события попарно не совместны, то

 Теорема: Системы аксиом 1,2,3,4 и 1,2,3* равносильны.
Теорема: Системы аксиом 1,2,3,4 и 1,2,3* равносильны.
Дата добавления: 2015-07-30; просмотров: 1702;
