Вероятности, вытекающие из аксиом.

1) Если из события А следует событие В ( 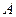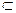B) то вероятность

Р(В\А)= Р(В)-Р(А)≥0

А∙(В\А)=0

Р(В)= Р(А) + Р(В\А)

2) А 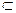В → Р(А)≤Р(В) (из А следует В)

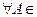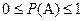3) А 0 < А < Ω

4) Р(0) = 0 0 + Ω = Ω

Р(0) + 1 = 1

5) 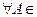А Р(А) + Р(Ā) = 1

6) Если события 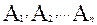попарно не совместны

то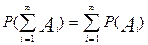

7) 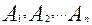произвольные события

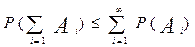
8) 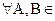А

∆ А + В = А + ( В \ А); А ∙ ( В \ А ) = 0

В Р(А+В)= Р(А) + Р( В \ А)

А В\А = В \ (АВ)

Р(В\А) = Р(В) – Р(АВ)

Р(А+В) = Р(А) + Р(В) – Р(АВ)▲

Замечания:

1. Формулы: Р(А+В) = Р(А) + Р(В); АВ = 0

Р(А+В) = Р(А) + Р(В) – Р(АВ); АВ ≠ 0

Называются формулами сложения вероятностей.

2. Аксиомы вероятности и их следствия имеют естественное обоснование в рамках классического подхода.

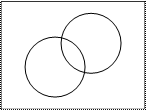Ω

к В

А м

L

n

Р(А+В) =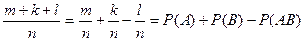

3. Р(А+В+С) = Р(А) + Р(В) + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + Р(АВС)

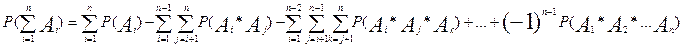
В случае если все события не совместны то

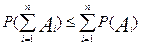
4. Если событие А достоверное то его вероятность равна 1

Р(А)=1 А→Р(А) = 1

Если А невозможное, вероятность его равна 0

Р(А)=0 А→Р(А) = 0

Обратные утверждения верны, только в случае конечного числа элементарных исходов.