Независимость событий.

Опр. 1:Два события называются независимыми если информация о том произошло или нет одно из них не влияет на вероятность другого.

Р(А)=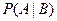

Р(В) =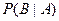

Опр. 2:Несколько событий называются попарно независимыми, если каждые два из них независимы.

Опр. 3: Несколько событий называются независимыми в совокупности, если они попарно независимы и каждое событие не зависит от всевозможных произведений остальных событий.

Пример: А,В,С – попарно независимы. Тогда независимы А и В, В и С,А и С. Если в совокупности, то А и В,В и С,А и С,А и ВС,В и АС,С и АВ.

Теорема 1: Если событие А и В независимы, то вероятность Р(АВ)=Р(А)∙Р(В)

Теорема 2: Если события , независимы в совокупности, то Р( ) =

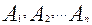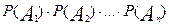
Пример 1: Есть 4 числа: 2,3,5,30

- вытащенное число делится на 2,3,5

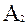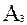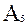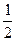
1)Р( )=Р( )=Р( )= 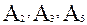попарно независимы

2)Р( )= =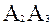

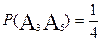
3) 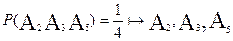в совокупности зависимы

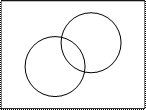
Пример 2:

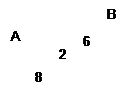24 24

Р(А) = 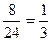Р(А) =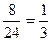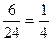

Р(В)= Р(В)=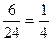

Р(АВ)= 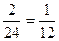Р(АВ)=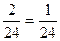

Р(АВ)=Р(А)∙Р(В) Р(АВ)≠Р(А)∙Р(В)

Это означает, что А и В независимы Это означает, что А и В зависимы

P(A)=P(A|B) P(A)≠P(A|B)

Пример 3: 1)Имеется колода карт из 36 карт

А – вытянули пику

В – вытянули даму

Р(А) Р(А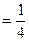В) = Р(А)∙Р(В) события независимы

Р(В)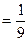

Р(АВ)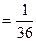

2) В колоду добавили джокера

Р(А) Р(АВ) ≠ Р(А)∙Р(В) события зависимы

Р(В)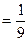

Р(АВ)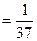

Замечание: при установлении независимости А и В часто используют следующий принцип: события А и В, реальные прообразы которых причинно независимы считаются независимыми и в теоретико-вероятностном смысле.