Алгебра событий.

Одним из основных понятий теории вероятностей является опыт. Под опытом понимается выполнение комплекса условий, в результате которого происходят или не происходят определенные события (факты). Событие это возможный результат опыта или испытания.

Простейшие неразложимые результаты опыта называются элементарными событиями (w_i), а вся совокупность элементарных событий называется пространством элементарных событий W={wi}. С каждым опытом связано свое пространство элементарных событий W.

Любое конечное или счетное подмножество W называется событием. Различают три типа событий:

1) достоверные (W),

2) случайные,

3) невозможные (Ø или ).

События обычно обозначают первыми прописными буквами латинского алфавита: А, В, С,…. Событие называется достоверным, если в результате опыта оно обязательно произойдет. Событие называется невозможным, если оно не может произойти в данном опыте. Случайным называется событие, которое в данном опыте может произойти, а может и не произойти..

События А и В несовместны, если в результате одного опыта они не могут происходить одновременно, в противном случае - совместны. Например, при одном подбрасывании монеты не могут одновременно появиться герб и решетка.

Элементы последовательности событий А₁, А₂,…,А_n попарно несовместны, если любые два из них несовместны. Например, при подбрасывании игральной кости никакие два элементарных исхода (появление цифр 1, 2, 3, 4, 5, 6) не могут произойти одновременно. Несколько событий равновозможные, если ни одно из них не является более возможным, чем другие. Несколько событий называются единственно возможными, если в результате испытания произойдет хотя бы одно из них.

События А₁,…,А_n образуют полную группу, если в результате опыта кроме этих событий ничего не может произойти, т. е. они являются несовместными и единственно возможными. Обычно W изображают на плоскости в виде некоторой области, а w_i в виде точек этой области, устанавливая, таким образом, соответствие между событиями и точечными множествами. Над событиями вводятся операции, совпадающие с операциями над множествами: сумма, произведение, отрицание. 1. Суммой событий А и В называется такое третье событие А+В (или АÈВ), которое заключается в наступлении хотя бы одного из событий или А, или В. 2. Произведением двух событий А и В называется такое третье событие АВ (или 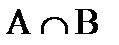), которое заключается в наступлении событий А и В одновременно. Если события А и В несовместны, то А×В=Æ . 3. Отрицанием события А называется событие 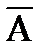(не А), заключающееся в не наступлении события А (А+ 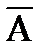=W, А× 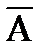= ). Причем, если в результате опыта может произойти событие А, то может произойти и обратное ему событие .

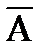Если наступление события А приводит к наступлению события В и наоборот (наступление В влечет наступление А), то события А и В равны (А=В).

Пусть S – множество всех подмножеств W, для которого выполняются следующие свойства:

1) если то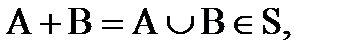

2) если 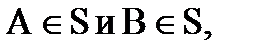то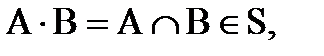

3) если 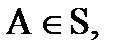то ,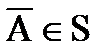

тогда множество S называется алгеброй событий.