Определения вероятности события.

Существует несколько подходов к определению вероятности события. Аксиоматическое определение вероятности.

Вероятность события - это численная мера объективной возможности его появления.

Аксиомы вероятности:

1. Каждому событию A ставится в соответствие неотрицательное число p, которое называется вероятностью события A:

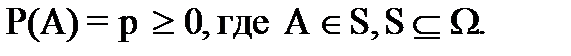
2. Если события 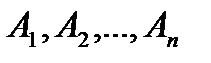несовместны, то верно равенство:

,

.

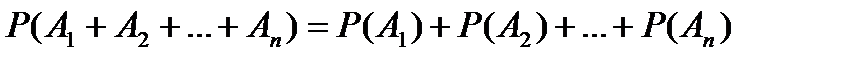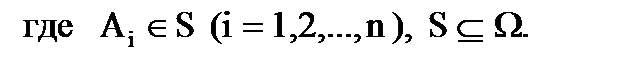3. P( ) = 1 ,

где - истинное (достоверное) событие.

Пространство элементарных событий W с заданной в нем алгеброй S (или s - алгеброй) и определенной на S вероятностью – неотрицательной мерой P(A), AÎS называется вероятностным пространством и обозначается (W, S, P). Вероятностное пространство служит математической моделью любого случайного явления в теории вероятностей.

Аксиоматический подход не указывает, как конкретно находить вероятность, поэтому для решения задач целесообразно использовать подходы к определению вероятности, которые перечислены ниже.

Классическое определение вероятности.

Пусть события 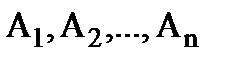ÎS (*)

образуют множество элементарных событий. Тогда события, из (*), которые приводят к наступлению события A, называются благоприятствующими исходами для события А, m(A) - число благоприятствующих исходов.

Вероятностью события А называется отношение числа исходов, благоприятствующих наступлению события А к числу всех возможных элементарных исходов

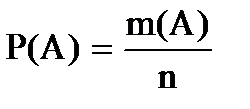. (1.1)

Из классического определения следуют свойства вероятности:

1) ,

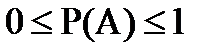2) P( )=1,

3) P( )=0.

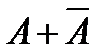= - достоверное событие, поэтому

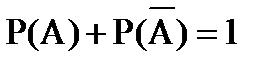или

Статистическое определение вероятности.

Пусть проводится серия опытов (n раз), в результате которой наступает или не наступает некоторое событие А (m раз), тогда отношение 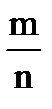, при 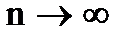, называется статистической вероятностью события А.

Иногда, при рассмотрении бесконечных множеств удобно рассматривать геометрическое определение вероятности.

Геометрическое определение вероятности.

Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области.