Элементы комбинаторики

Комбинаторика (комбинаторный анализ) - раздел дискретной математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами.

Правило произведения. Пусть из некоторого конечного множества

1-й объект можно выбрать к ₁ способами,

2-ой объект - к ₂ способами,

…..………………………...…, (1.2)

n-ый объект - к _n способами.

Тогда произвольный набор, перечисленных n объектов, из данного множества можно выбрать к₁·к₂·…·к_n способами.

Правило суммы. При выполнении условий (1.2), любой из объектов можно выбрать к₁ + к₂ + к₃ + …+ к_n способами.

Обычно в комбинаторике рассматривается идеализированный эксперимент по выбору наудачу к элементов из n. При этом элементы: а) не возвращаются обратно (схема выбора без возвращений); б) возвращаются обратно (схема выбора с возвращением).

I. Схема выбора без возвращений. Размещением из n элементов по к называют любой упорядоченный набор из к элементов, принадлежащих n элементному множеству. Различные размещения отличны друг от друга или порядком элементов, или составом.

Число размещений из n элементов по к обозначается 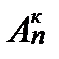и вычисляется по формуле

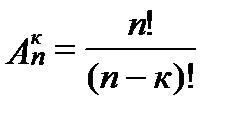, (1.3)

где n!= 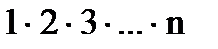, 1!=1 , 0!=1.

Перестановкой из n элементов называют размещение из n элементов по n. Перестановки отличаются друг от друга порядком своих элементов. Число перестановок из n элементов обозначают Р_n и вычисляют по формуле

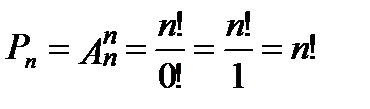. (1.4)

Сочетанием из n элементов по к называется любой набор из к элементов, принадлежащих n элементному множеству. Различные сочетания отличаются друг от друга только составом своих элементов.

Число сочетаний из n элементов по к обозначается 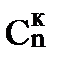и вычисляется по формуле

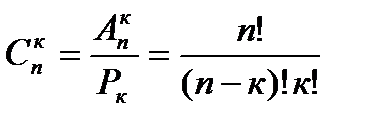. (1.5)

Справедливы тождества:

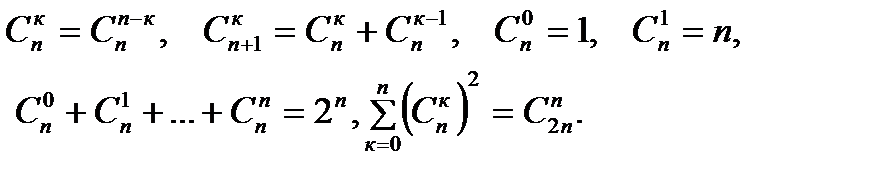(1.6)

II.Схема выбора с возвращениями. Если при выборе к элементов из n - элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями.

Число размещений с повторениями

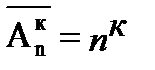. (1.7)

Если при выборе к элементов из n элементы возвращаются обратно без последующего упорядочивания, то говорят, что это сочетания с повторениями. Число сочетаний с повторениями из n элементов по к

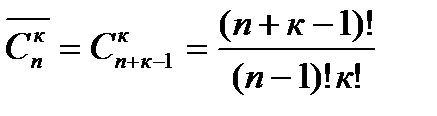. (1.8)

III. Схема упорядоченных разбиений. Пусть к₁,к₂,…,к_r – целые числа, такие, что к₁ + к₂+…+к_r=n, к_i³0 (i=1,2,...,r).Число способов, которыми генеральную совокупность из n элементов можно разделить на r упорядоченных частей (r подмножеств или r групп), из которых первая содержит к₁ элементов, вторая - к₂ элементов и r-тая - к_r элементов обозначается С_n (к₁, к₂,…, к_r) и вычисляется по формуле

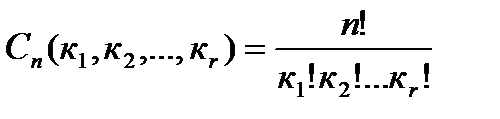. (1.9)

Числа, которые определяются по формуле (1.9), называются полиномиальными коэффициентами.