Формула Бернулли.
Постоянные условия опыта. а) Пусть некоторый опыт повторяется в неизменных условиях n раз, причём каждый раз может либо наступить (успех), либо не наступить (неудача) некоторое событие А, где Р(А)=р − вероятность успеха, Р(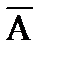 
)= 1- р= q – вероятность неудачи. Тогда вероятность того, что в к случаях из n произойдёт событие А вычисляется по формуле Бернулли:
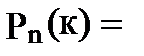
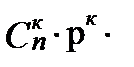
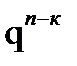. (1.24)
Условия, приводящие к формуле Бернулли, называются частной схемой повторных независимых испытаний или схемой Бернулли. Так как вероятности Pn(к) для различных значений к представляют собой слагаемые в разложении бинома Ньютона:
+ 
+… 
+…+ 
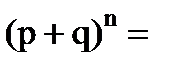
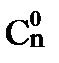
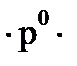
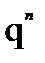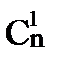
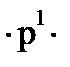
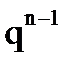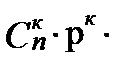
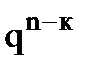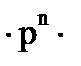
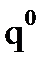, то распределение вероятностей Pn(к), где 
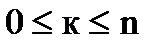, называется биномиальным.
Переменные условия опыта. Если в каждом из независимых испытаний вероятности наступления события А разные (общая схема повторения опытов), то вероятность наступления события А к раз в n опытах, определяется как коэффициент, при к-ой степени полинома
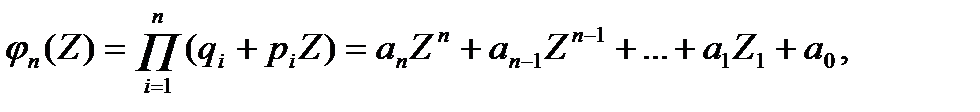(1.25)
jn(Z) – производящая функция.
Дата добавления: 2015-08-11; просмотров: 709;