Интегральная теорема Муавра-Лапласа. Пуассоновское приближение
Формула Пуассона.
Если вероятность р наступления события А в каждом испытании постоянна и стремится к нулю, а число испытаний достаточно велико (npq<10 и p<0,1), то вероятность того, что событие А появится к раз в п независимых испытаниях приближенно равна
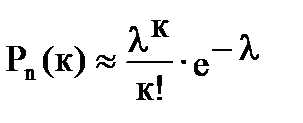 , (1.30)
, (1.30)
где 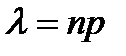 .
.
При больших значениях n , для вычисления вероятности того, что произойдет от к1 до к2 событий в п независимых испытаниях по схеме Бернулли, используется интегральная формула Муавра-Лапласса:
Рn ( 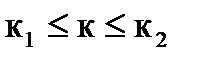 )=Ф(x2) - Ф(x1), (1.31)
)=Ф(x2) - Ф(x1), (1.31)
где x1 = 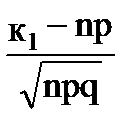 , x2 =
, x2 = 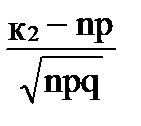 , Ф(х) - функция Лапласа.
, Ф(х) - функция Лапласа.
Ф(x) имеет следующие свойства:
1) Ф(-x)= -Ф(x) – функция нечетная, поэтому достаточно применять её для неотрицательных значений x:
Ф(x)= 
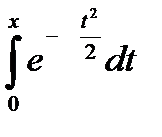 ; (1.32)
; (1.32)
2) функция Ф(x) возрастает на всей числовой оси;
3) при x 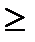 4, Ф(x)®
4, Ф(x)® 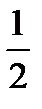 ( y=0,5- горизонтальная асимптота при x>0), поэтому функция представлена в виде таблицы для
( y=0,5- горизонтальная асимптота при x>0), поэтому функция представлена в виде таблицы для 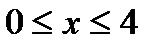 ;
;
Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях не более чем на некоторое число e>0:
Рn 
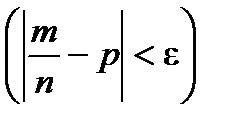 = 2Ф
= 2Ф 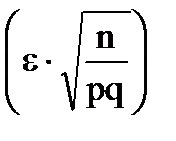 . (1.33)
. (1.33)
Дата добавления: 2015-08-11; просмотров: 1053;
