Вычисление ускорения. Теорема Гюйгенса
Обратимся теперь к выводу формулы для вычисления ускорения  материальной точки.
материальной точки.
По определению ускорения имеем
 .
.
Заменяя в правой части  на
на  , и дифференцируя по
, и дифференцируя по 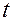 , получим
, получим
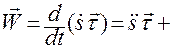
 .
.
Воспользуемся формулой Френе
 ,
,
где
 – орт главной нормали к траектории в том положении, которое занимает на ней точка
– орт главной нормали к траектории в том положении, которое занимает на ней точка  в момент времени
в момент времени 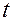 ;
;
 – кривизна траектории;
– кривизна траектории;
 – радиус кривизны траектории в этом положении.
– радиус кривизны траектории в этом положении.
Тогда выражение для  примет вид:
примет вид:
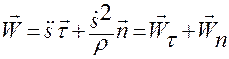 . (1.2.16)
. (1.2.16)
Вектор
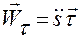
называется касательным (тангенциальным) ускорением точки  .
.
Вектор

называется нормальным ускорением точки  .
.
Величина скорости обозначена
 .
.
Формула (1.2.16) составляет предмет теоремы Гюйгенса.
Дата добавления: 2015-08-21; просмотров: 1739;
