Способы задания кривой
Как показано в главе 1, §2, пункт 1 , траектория движения материальной точки, задаваемая при описании его естественным способом, представляет собой кривую линию в трехмерном пространстве 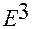 с системой отсчета
с системой отсчета 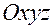 .
.
Поэтому требование задать траекторию означает, что надо задать кривую в трехмерном пространстве.
Как известно из дифференциальной геометрии, кривая в пространстве 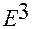 с системой координат
с системой координат 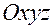 может быть задана одним из следующих способов:
может быть задана одним из следующих способов:
· векторный,
· параметрический,
· явное задание кривой,
· неявное задание кривой.
1). Векторный способ
Задается векторная функция 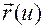 ,
, 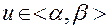 и полагается
и полагается
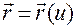 . (1.2.2)
. (1.2.2)
Здесь
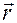 — радиус-вектор точки на кривой,
— радиус-вектор точки на кривой,
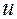 — параметр, принимающий все значения из промежутка
— параметр, принимающий все значения из промежутка 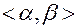 .
.
Векторная функция 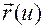 называется параметризацией кривой.
называется параметризацией кривой.
Если сделаем замену
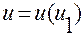 ,
,  ,
,
при которой промежуток 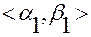 изменения параметра
изменения параметра 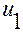 однозначно отображается в промежуток
однозначно отображается в промежуток 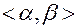 изменения параметра
изменения параметра 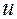 , то подстановкой
, то подстановкой 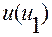 в (1.2.2)
в (1.2.2)
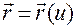 (1.2.2)
(1.2.2)
получим
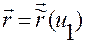 ,
,  , (1.2.3)
, (1.2.3)
где
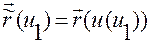 .
.
Соотношение (1.2.3) задает геометрически ту же кривую, что и соотношение (1.2.2).
В таком случае говорят, что данная кривая задается в параметризации 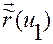 .
.
2). Параметрический способ
В декартовой прямоугольной системе координат 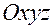 задаются координаты точки на кривой
задаются координаты точки на кривой
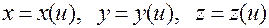 ,
, 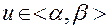 .
.
3). Явное задание кривой
В декартовой прямоугольной системе координат 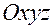 оно имеет вид:
оно имеет вид:
· на плоскости 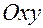
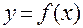 ,
, 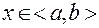 ;
;
· в пространстве 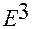
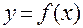 ,
, 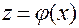 ,
, 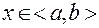 .
.
При явном задании кривой роль параметра играет одна из координат (в указанном здесь задании — это координата 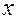 ).
).
4). Неявное задание кривой
Такое задание имеет вид:
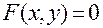 – на плоскости
– на плоскости 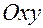 ;
;
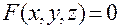 ,
, 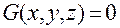 — в пространстве
— в пространстве 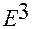 в ДПСК
в ДПСК 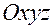 .
.
Дата добавления: 2015-08-21; просмотров: 4817;
