Вычисление скорости
По определению скорости материальной точки можем записать
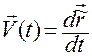 .
.
Здесь
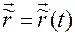 – движение точки
– движение точки  , заданное векторным способом;
, заданное векторным способом;
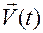 – ее скорость в момент времени
– ее скорость в момент времени 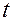 .
.
Согласно связи векторного способа с естественным имеем
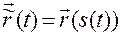 ,
,
где
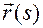 – естественная параметризация траектории движения,
– естественная параметризация траектории движения,
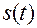 – закон движения по этой траектории.
– закон движения по этой траектории.
Дифференцируя 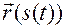 по
по 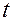 , получаем
, получаем
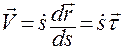 , (1.2.15)
, (1.2.15)
где
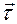 — орт касательной к траектории в той ее точке, с которой совпадает положение материальной точки
— орт касательной к траектории в той ее точке, с которой совпадает положение материальной точки  в момент времени
в момент времени 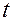 .
.
Из (1.2.15) можем сделать следующие заключения:
а) скорость 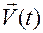 параллельна
параллельна 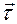 — орту касательной к траектории в том положении точки
— орту касательной к траектории в том положении точки  , которое она занимает, находясь на траектории в момент времени
, которое она занимает, находясь на траектории в момент времени 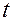 ;
;
б) 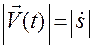 .
.
Дата добавления: 2015-08-21; просмотров: 971;
