Вероятность отклонения частоты от постоянной вероятности в независимых событий. Асимптотическая формула Пуассона

Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты 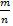от постоянной вероятности p по абсолютной величине не превышает заданного числа 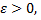т.е. найдем вероятность осуществления неравенства

,

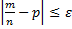т.е.

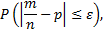
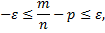
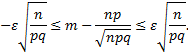
Используя интегральную формулу Лапласа, получим

.

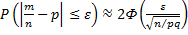Рассмотрим пример. Вероятность того, что деталь не стандартна 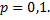Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности 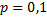по абсолютной величине не более, чем на 0,03.

Используя формулу

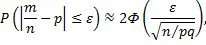
получим

,

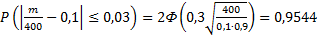т.к. .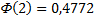

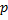Пусть производится n независимых испытаний, в каждом из которых вероятность появления события равна . Для определения вероятности m появлений события в этих испытаниях используют формулу Бернулли. Если 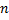– велико, то пользуются формулой Лапласа. Если же вероятность события мала 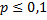, то прибегают к формуле Пуассона. Важное допущение

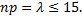
Асимптотическое представление вероятности 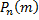посредством функции

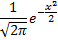
действует тем хуже, чем больше вероятность 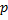отличается от половины, т.е. чем меньшие значения 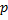или 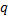приходится рассматривать, и это представление отказывается служить при 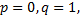а также при 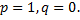Но, значительный круг задач связан с необходимостью вычисления вероятностей 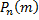при малых значениях 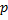или 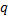. Для того, чтобы в этом случае теорема Лапласа дала результат с незначительной ошибкой, необходимо, чтобы число n испытаний было очень велико. Формула для разыскания асимптотической формулы, специально приспособленной для случая малых 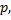была найдена Пуассоном

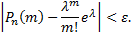
Теорема Пуассона имеет место и в том случае, когда вероятность события в каждом испытании равна нулю (в этом случае 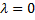). Принято обозначение

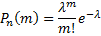
- это есть распределение вероятностей по закону Пуассона.

Рассмотрим пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится 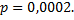Требуется найти вероятность того, что на базу прибудут 3 негодных изделия.

Вероятность очень мала, а число испытаний достаточно велико, выполняется условие

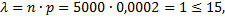
следовательно, возможно применить формулу Пуассона

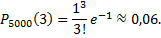
Контрольные вопросы

1. С помощью какой формулы можно найти вероятность появления события А определенное количество раз при n испытаниях?

2. Почему не всегда возможно применить формулу Бернулли?

3. В каких задачах используют формулу Пуассона?

4. Как решается задача нахождения вероятности того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превышает заданного числа?