Локальная теорема Лапласа. Интегральная теорема Лапласа
Локальная теорема Лапласа дает формулу, которая позволяет приближенно найти вероятность появления события ровно m раз в n испытаниях, если число испытаний достаточно велико.
Теорема Лапласа: если вероятность p появления события  в каждом испытании постоянна и отлична от нуля, то вероятность
в каждом испытании постоянна и отлична от нуля, то вероятность 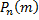 того, что событие
того, что событие  появится в n испытаниях ровно
появится в n испытаниях ровно 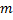 раз, приближенно равна
раз, приближенно равна
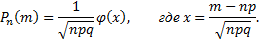
Рассмотрим пример. Вероятность поражения мишени стрелком при одном выстреле 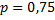 . Найти вероятность того, что при 10 выстрелах стрелок поразит мишень ровно 8 раз.
. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень ровно 8 раз.
Используя формулу Лапласа, получим
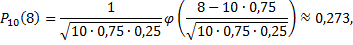
так как 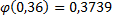 согласно таблице функции Лапласа.
согласно таблице функции Лапласа.
Предположим, что производится n испытаний, в каждом из которых вероятность появления события  постоянна и равна
постоянна и равна 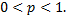 Как вычислить вероятность того, что событие
Как вычислить вероятность того, что событие  появится в
появится в  испытаниях не менее
испытаниях не менее 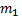 раз и не более
раз и не более 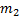 раз?
раз?
Интегральная теорема Лапласа: если вероятность 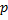 наступления события
наступления события  в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
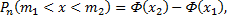
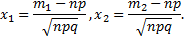
Ф(x) – интегральная функция Лапласа, которая равна
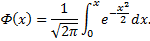
Рассмотрим пример. Вероятность того, что деталь не прошла проверку ОТК, равна 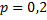 . Найти вероятность того, что среди 400 случайно отобранных деталей окажется не проверенных от 70 до 100 деталей.
. Найти вероятность того, что среди 400 случайно отобранных деталей окажется не проверенных от 70 до 100 деталей.
Согласно тем данным, которые даны в задаче, можно, используя интегральную формулу Лапласа найти искомую вероятность
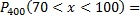
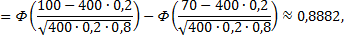
так как
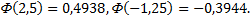
Дата добавления: 2015-08-11; просмотров: 1206;
