Формула полной вероятности. Формулы Байеса

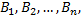Вероятность события , которое может наступить лишь при условии появления одного из несовместных событий образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события

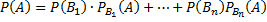
- это есть формула полной вероятности.

Рассмотрим пример. Электролампы изготавливают на трех заводах. Первый завод производит 35% общего количества электроламп, второй – 50% и третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80% и третьего – 90%. В магазин поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа является стандартной?

Примем за событие – лампа, купленная в магазине стандартная; – купленная лампа с первого завода; 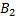- купленная лампа со второго завода; 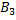- купленная лампа с третьего завода.

Тогда можно записать

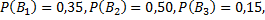
Воспользуемся формулой полной вероятности

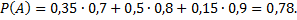
Рассмотрим еще один пример. В первой коробке содержится 20 деталей, из них 18 стандартных; во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята деталь и переложена в первую. Найти вероятность того, что деталь, наудачу извлеченная из первой коробки, будет стандартной.

Примем за событие – из первой коробки извлечена стандартная деталь; – из второй коробки извлечена стандартная деталь; 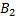– из второй коробки извлечена нестандартная деталь. Тогда

Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была положена стандартная деталь

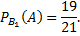
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была положена нестандартная деталь

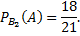
Тогда

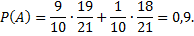
Пусть событие А может наступить при условии появления одного из несовместных событий 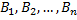, образующих полную группу (гипотезы).

Допустим, что произведено испытание, в результате которого появилось событие . Определим, как изменились (в связи с тем, что событие уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

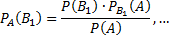
– это есть формулы Байеса, которые позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие .

Рассмотрим пример. С первого автомата поступает на сборку 80% деталей, а со второго – 20%. На первом автомате брак составляет 1%, а на втором – 5%. Проверенная деталь оказалась бракованной. Что вероятнее: проверенная деталь изготовлена на первом автомате или на втором?

Примем за событие – проверенная деталь бракованная; 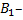проверенная деталь с первого автомата; 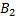– проверенная деталь со второго автомата. Таким образом,

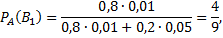
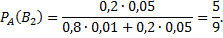
Таким образом, вероятнее, что деталь изготовлена на втором заводе.

Контрольные вопросы

1. Дать определение случайного события. Почему события представляются нам случайными?

2. Какие события называются достоверными, равновозможными, совместными, независимыми?

3. Дать классическое определение вероятности.

4. В чем принципиальное отличие понятия вероятности события и относительной частоты появления события?

5. Сформулировать теорему сложения вероятностей для несовместных, совместных событий.

6. Сформулировать теорему умножения вероятностей.

7. Что Вы понимаете под условной вероятностью события?