Формула Бернулли
Если производится несколько испытаний, причем вероятность события  в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события
в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события  . Рассмотрим независимые испытания, в котором событие
. Рассмотрим независимые испытания, в котором событие  имеет одну и ту же вероятность.
имеет одну и ту же вероятность.
Пусть производится n независимых испытаний, в каждом из которых событие  может появиться либо не появиться. Условимся считать, что вероятность события
может появиться либо не появиться. Условимся считать, что вероятность события  в каждом испытании одна и та же, а именно –
в каждом испытании одна и та же, а именно – 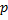 . Следовательно, вероятность не наступления события
. Следовательно, вероятность не наступления события  равна
равна 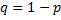 .
.
Перед нами будет стоять задача найти вероятность того, что при n испытаниях событие  осуществится
осуществится 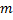 раз, следовательно, не осуществится
раз, следовательно, не осуществится 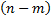 раз. Не требуется, чтобы событие
раз. Не требуется, чтобы событие  повторилось ровно
повторилось ровно 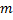 раз в определенной последовательности. Искомую вероятность обозначим
раз в определенной последовательности. Искомую вероятность обозначим 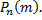
Поставленную задачу можно решить с помощью формулы Бернулли.
Вероятность одного сложного события, состоящего в том, что в n испытаниях событие  наступит m раз и не наступит
наступит m раз и не наступит 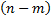 раз, по теореме умножения вероятностей независимых событий равна
раз, по теореме умножения вероятностей независимых событий равна
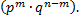
Таких сложных событий может быть столько, сколько можно составить сочетаний из 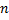 элементов по
элементов по  элементов, т.е.
элементов, т.е. 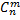 . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий, искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку вероятности всех этих сложных событий одинаковы, то
. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий, искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку вероятности всех этих сложных событий одинаковы, то
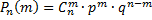
– это есть формула Бернулли.
Рассмотрим пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна 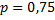 . Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Вероятность нормального расхода электроэнергии в продолжение суток равна 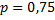 , следовательно
, следовательно
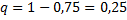 .
.
Тогда, используя формулу Бернулли, можно найти искомую вероятность
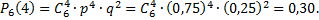
Дата добавления: 2015-08-11; просмотров: 1820;
