Теорема сложения вероятностей для совместных событий

Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

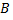Пусть события и совместны, причем даны вероятности этих событий и вероятность их совместного появления. Как найти вероятность события 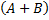, состоящего в том, что появится хотя бы одно из событий и 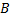? Ответ на этот вопрос дает теорема сложения вероятностей совместных событий.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

При использовании полученной формулы следует иметь в виду, что события и 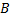могут быть как независимыми, так и зависимыми.

Для независимых событий

Для зависимых событий

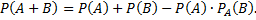
Если события и 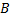несовместны, то их совмещение есть невозможное событие и, следовательно,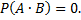

Рассмотрим пример. Вероятности попадания в цель при стрельбе первого и второго орудий совместно равны:

Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

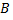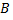Примем за – попадание с 1-го орудия, за – попадание из 2-го орудия, и – события независимые. Следовательно,

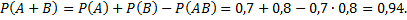
Пусть событие может наступить при условии появления одного из несовместных событий 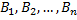, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности 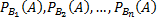события .