Свойства функции распределения и функции плотности распределения вероятности появления случайной величины

Свойства функции распределения.

1)Значения функции распределения принадлежат отрезку

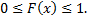
2) 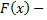неубывающая функция, т.е.

если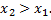

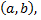Если положить то вероятность того, что случайная величина примет значение, заключенное в интервале равна приращению функции распределения на этом интервале:

Вероятность того, что непрерывная случайная величина 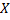примет одно определенное значение, равна нулю. Таким образом, имеет смысл рассматривать вероятность попадания в интервал (даже сколь угодно малый), а не вероятность того, что непрерывная случайная величина примет одно определенное значение. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, а не вероятностью их совпадения с проектным размером.

3)Если возможные значения случайной величины принадлежат интервалу 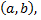то

при при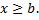

Вышеперечисленные свойства позволяют представить вид графика функции распределения непрерывной случайной величины:

1) график ограничен прямыми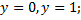

2) при ординаты графика равны нулю;

3) при ординаты графика равны единице;

4) при возрастании в интервале 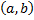, в котором заключены все возможные значения случайной величины, график возрастает.

Рис. 73

График функции распределения непрерывной случайной величины

График функции распределения дискретной случайной величины имеет ступенчатый вид.

Рассмотрим пример. Дискретная случайная величина задана таблицей распределения, начертить график .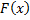

	0,084	0,302	0,380	0,198	0,036

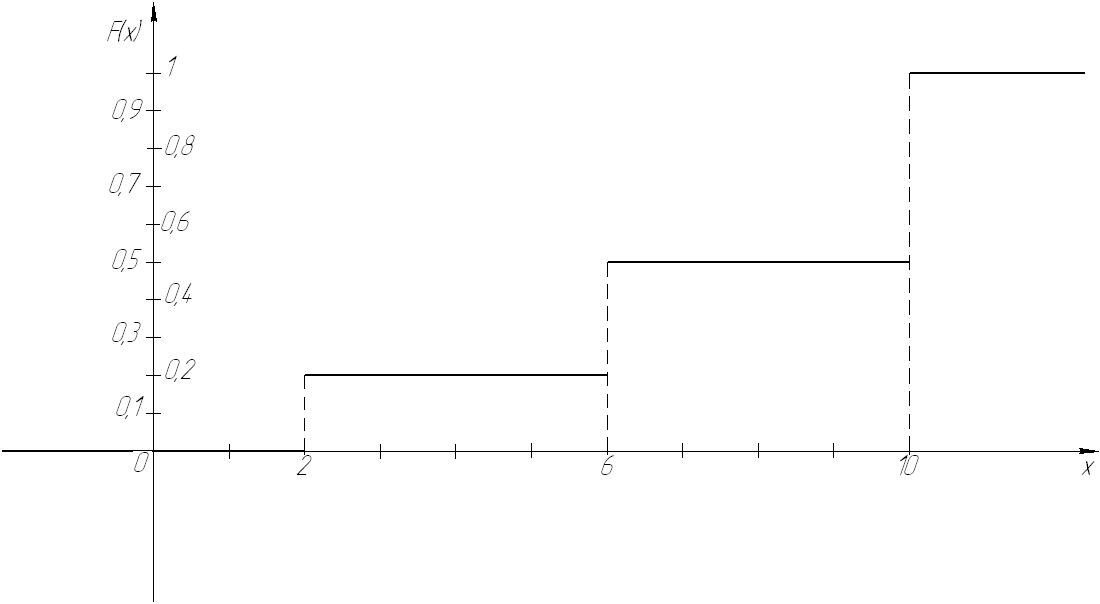
Рис. 74

График функции распределения дискретной случайной величины

Свойства функции плотности распределения вероятностей.

1)Плотность распределения неотрицательная функция

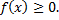
2)Несобственный интеграл от плотности распределения в пределах от 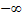до 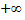равен единице

3)Если все возможные значения непрерывной случайной величины принадлежат интервалу 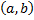, то

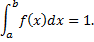
Вероятностный смысл функции плотности распределения вероятностей: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу 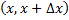, приближенно равна произведению плотности вероятности в точке на длину интервала Геометрически этот факт можно растолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу

приближенно равна площади прямоугольника с основанием и высотой .