Вероятность попадания случайной величины на заданный интервал
Вероятность того, что непрерывная случайная величина  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 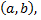 равна определенному интегралу от плотности распределения, взятому в пределах от
равна определенному интегралу от плотности распределения, взятому в пределах от  до
до 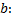
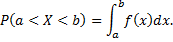
Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу 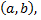 равна площади криволинейной трапеции, ограниченной осью
равна площади криволинейной трапеции, ограниченной осью 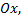 кривой распределения
кривой распределения  и прямыми
и прямыми 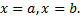
Рассмотрим пример. Задана плотность вероятности случайной величины 

Найти вероятность того, что в результате испытания 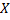 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 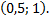
Искомая вероятность
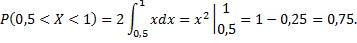
Дата добавления: 2015-08-11; просмотров: 1132;
