Распределение Пуассона дискретной случайной величины. Простейший поток событий
Если стоит задача найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно  раз. Сделаем важное допущение: произведение
раз. Сделаем важное допущение: произведение 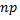 сохраняет постоянное значение, а именно
сохраняет постоянное значение, а именно 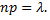 Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях
Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях 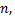 остается неизменным.
остается неизменным.
Воспользуемся формулой Бернулли для вычисления, интересующей нас вероятности
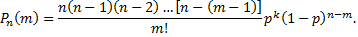
Так как 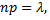 то
то
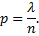
Следовательно,
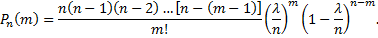
Примем во внимание, что  имеет очень большое значение, вместо
имеет очень большое значение, вместо 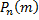 найдем
найдем
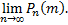
При этом будет найдено лишь приближенное значение отыскиваемой вероятности. Итак,
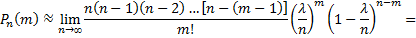

Таким образом,
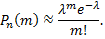
Эта формула выражает закон распределения Пуассона вероятностей массовых (  велико) и редких (
велико) и редких ( 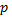 мало) событий.
мало) событий.
Рассмотрим события, которые наступают в случайные моменты времени.
Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Примерами потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, последовательность отказов элементов.
Среди свойств, которыми могут обладать потоки, выделяют свойства стационарности, отсутствие последствия и ординарности.
Свойство стационарности характеризуется тем, что вероятность появления  событий на любом промежутке времени зависит только от числа
событий на любом промежутке времени зависит только от числа  и от длительности
и от длительности 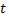 промежутка и не зависит от начала отсчета.
промежутка и не зависит от начала отсчета.
Если поток обладает свойством стационарности, то вероятность появления  событий за промежуток времени длительности
событий за промежуток времени длительности 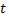 есть функция, зависящая только от
есть функция, зависящая только от  и
и 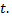
Свойство отсутствия последствия характеризуется тем, что вероятность появления  событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка.
событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка.
Если поток обладает свойством отсутствия последействия, то имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени.
Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно.
Если поток обладает свойством ординарности, то за бесконечно малый промежуток времени может появиться не более одного события.
Простейшим называют поток событий, который обладает свойством стационарности.
Интенсивностью потока 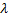 называют среднее число событий, которые появляются в единицу времени.
называют среднее число событий, которые появляются в единицу времени.
Если постоянная интенсивность потока известна, то вероятность появления  событий простейшего потока за время длительностью
событий простейшего потока за время длительностью 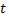 определяется формулой Пуассона
определяется формулой Пуассона
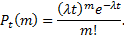
Формулу Пуассона можно считать математической моделью простейшего потока событий.
Рассмотрим пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятности того, что за 5 минут поступит 2 вызова.
По условию,  Воспользуемся формулой Пуассона
Воспользуемся формулой Пуассона
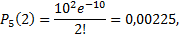
т.е. событие практически невозможно.
Пусть производятся независимые испытания, в каждом из которых вероятность появления события  равна
равна 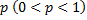 и, следовательно, вероятность его непоявления
и, следовательно, вероятность его непоявления
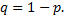
Испытания заканчиваются, как только появится событие 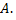 Таким образом, если событие
Таким образом, если событие  появилось в
появилось в 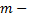 м испытании, то в предшествующих
м испытании, то в предшествующих 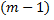 испытаниях оно не появлялось.
испытаниях оно не появлялось.
Обозначим через  дискретную случайную величину – число испытаний, которые нужно провести до первого появления события
дискретную случайную величину – число испытаний, которые нужно провести до первого появления события  Очевидно, возможными значениями
Очевидно, возможными значениями  являются натуральные числа:
являются натуральные числа: 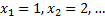
Пусть в первых 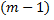 испытаниях событие
испытаниях событие  не наступило, а в
не наступило, а в 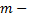 м испытании появилось. Вероятность этого события, по теореме умножения вероятностей независимых событий,
м испытании появилось. Вероятность этого события, по теореме умножения вероятностей независимых событий,

Полагая 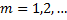 получим геометрическую прогрессию с первым членом
получим геометрическую прогрессию с первым членом 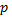 и знаменателем
и знаменателем 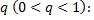

Рассмотрим пример.
Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель 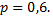 Найти вероятность того, что попадание произойдет при третьем выстреле.
Найти вероятность того, что попадание произойдет при третьем выстреле.
По условию 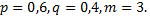 Искомая вероятность
Искомая вероятность
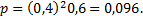
Распределение вероятностей, которое называют гипергеометрическим, определяет формула
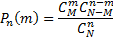
вероятность равна отношению числа исходов, благоприятствующих событию 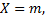 к числу всех элементарных исходов.
к числу всех элементарных исходов.
Пусть в партии из 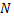 изделий имеется
изделий имеется 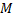 стандартных
стандартных 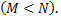 Из партии случайно отбирают
Из партии случайно отбирают  изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию. Обозначим через
изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию. Обозначим через  случайную величину – число
случайную величину – число  стандартных изделий среди
стандартных изделий среди  отобранных. Возможные значения
отобранных. Возможные значения  Найдем вероятность того, что
Найдем вероятность того, что 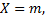 т.е. что среди
т.е. что среди  отобранных изделий ровно
отобранных изделий ровно  стандартных. Для этого будем использовать классическое определение вероятности.
стандартных. Для этого будем использовать классическое определение вероятности.
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь  изделий из
изделий из 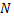 изделий, т.е. числу сочетаний
изделий, т.е. числу сочетаний 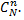
Число исходов благоприятствующих событию 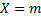 находят следующим образом:
находят следующим образом:  стандартных изделий можно извлечь из
стандартных изделий можно извлечь из 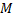 стандартных изделий
стандартных изделий 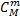 способами; взять
способами; взять  нестандартных изделий из
нестандартных изделий из 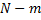 нестандартных изделий можно
нестандартных изделий можно 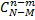 способами. Тогда, число благоприятствующих событию
способами. Тогда, число благоприятствующих событию 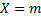 , равно
, равно 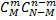 .
.
Рассмотрим пример. Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наудачу извлеченных 5 изделий окажется ровно 3 окрашенных.
По условию,
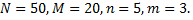
Искомая вероятность будет равна
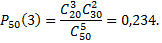
Дата добавления: 2015-08-11; просмотров: 1443;
