Нормальный закон распределения непрерывной случайной величины
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью распределения вероятностей
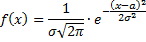
т.е. распределение определяется двумя параметрами 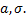
Вероятностный смысл этих параметров: 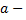 математическое ожидание;
математическое ожидание; 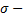 среднее квадратическое отклонение нормально распределенной случайной величины
среднее квадратическое отклонение нормально распределенной случайной величины
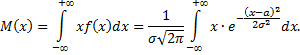
Введем новую переменную


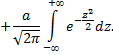
Первое слагаемое равно нулю (так как под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат); второе слагаемое – интеграл Пуассона
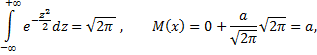
т.е. математическое ожидание нормального распределения равно параметру 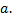
По определению дисперсия непрерывной случайной величины, учитывая, что 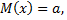 определяется формулой
определяется формулой
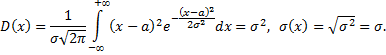
График плотности нормального распределения называют нормальной кривой (кривой Гаусса) (рис. 76).
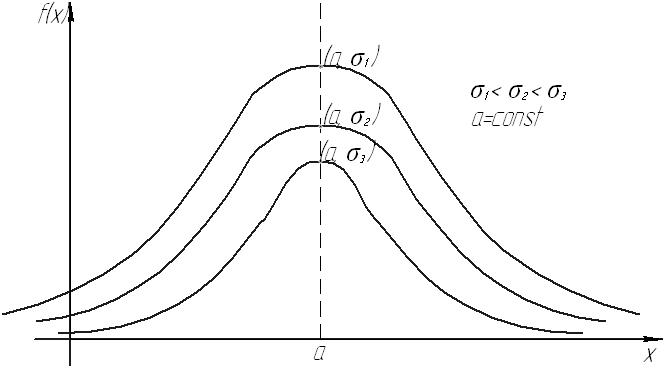
Рис. 76
Кривая Гаусса
Изменение величины параметра  не изменяет формы нормальной кривой, а приводит лишь к сдвигу вдоль оси
не изменяет формы нормальной кривой, а приводит лишь к сдвигу вдоль оси 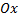 вправо, если
вправо, если  возрастает, и влево, если
возрастает, и влево, если  убывает. Максимум дифференциальной функции нормального распределения равен
убывает. Максимум дифференциальной функции нормального распределения равен
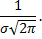
Следовательно, с возрастанием 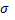 максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси
максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси 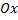 ; при убывании
; при убывании 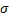 нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси
нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси 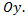
При любых значениях параметров 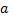 и
и 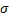 площадь ограниченная нормальной кривой и осью
площадь ограниченная нормальной кривой и осью 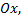 остается равной единице. При
остается равной единице. При 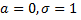 нормальную кривую называют нормированной
нормальную кривую называют нормированной
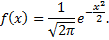
Вероятность попадания в заданный интервал
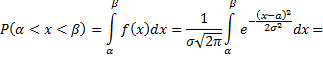

Рассмотрим пример. Случайная величина  распределена по нормальному закону. Математическое ожидание
распределена по нормальному закону. Математическое ожидание  Найти вероятность того, что
Найти вероятность того, что  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 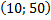
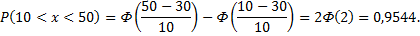
Дата добавления: 2015-08-11; просмотров: 1015;
