Вычисление вероятности заданного отклонения. Правило трех сигм

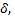Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины по абсолютной величине меньше заданного положительного числа т.е. требуется найти вероятность осуществления неравенства

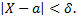
Перейдем к двойному неравенству

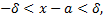
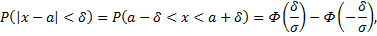
так как

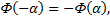
то

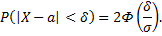
События, состоящие в осуществление неравенств

противоположные.

Поэтому, если вероятность осуществления неравенства

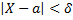
равна 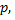то вероятность неравенства

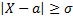
равна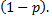

Рассмотрим пример. Случайная величина распределена нормально. Математическое ожидание и среднее квадратическое отклонение соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

По условию

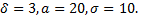
Тогда

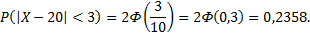
Правило трех сигм.

Преобразуем формулу

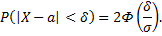
Пусть 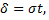тогда

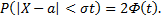
Если 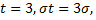то

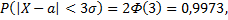
т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно 0,0027.

В этом и состоит правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике применяют правило трех сигм в случаях: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая случайная величина распределена нормально; в противном случае, случайная величина не распределена нормально.

Контрольные вопросы

1. Сформулировать понятие потока событий.

2. Записать аналитически и изобразить графически нормальный, равномерный и показательный законы распределения.

3. В чем состоит смысл правила трех сигм?