Центральная предельная теорема Ляпунова

Теорема Ляпунова: если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение близкое к нормальному.

Например. Пусть производится измерение некоторой физической величины. Любое измерение дает лишь приближенное значение измеряемой величины, так как на результат измерения влияют очень многие независимые случайные факторы (температура, колебания прибора, влажность и т.д.). Каждый из этих факторов порождает «частную ошибку». А так как число этих факторов очень велико, их совокупное действие порождает «суммарную ошибку».

Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок. Правомерно заключить, что суммарная ошибка имеет распределение близкое к нормальному.

Пусть последовательность независимых случайных величин, каждая из которых имеет математическое ожидание и дисперсию

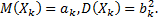
Пусть

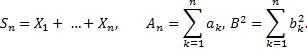
Обозначим функцию распределения нормированной суммы через

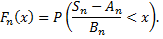
К последовательности 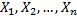применима теорема Ляпунова, если при любом функция распределения нормированной суммы при 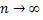стремится к нормальной функции распределения

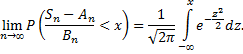
Условие Ляпунова: каждое слагаемое суммы

оказывало бы на сумму ничтожное влияние.