Применение закона больших чисел и центральной предельной теоремы

Научная ценность исследования Ляпунова, Чебышева и Маркова состоит в том, что они не только подметили эмпирическую устойчивость средних, но и нашли общие условия, выполнение которых обязательно влечет за собой статистическую устойчивость средних.

Наиболее общим законом больших чисел является теорема Чебышева, простейшим – Бернулли.

Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин

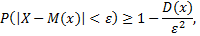
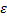- вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не меньше положительного числа , не меньше, чем

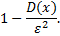
Теорема Чебышева: если 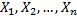- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают 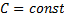), то, как бы мало ни было положительное число 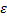, вероятность неравенства

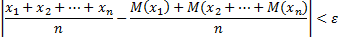
будет как угодно близка к единице, если число случайных величин достаточно велико. То есть

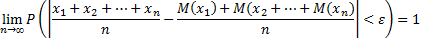
Сущность теоремы Чебышева состоит в том, что нельзя предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое. Среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины.

Теорема Бернулли: если в каждом из независимых испытаний вероятность 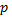появления события постоянна, то, как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности 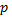по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико

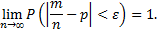
Неравенство Маркова

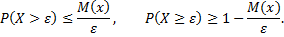
Для положительного числа 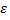данное неравенство верно, если случайная величина принимает только неотрицательное значение и имеет математическое ожидание.

Рассмотрим пример. Используя неравенство Чебышева, оценить вероятность того, что 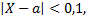если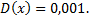

Решение:

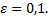
Согласно неравенству Чебышева, имеем

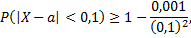
Рассмотрим пример. Вероятность выхода с автомата стандартной детали равна 0,96. Оценить с помощью неравенства Чебышева вероятность того, что число бракованных деталей среди 2000 находится в границах от 60 до 100 (включительно). Уточнить вероятность того же события с помощью интегральной теоремы Муавра-Лапласа. Объяснить различие полученных результатов.

Решение: вероятность того, что деталь бракованная

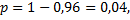
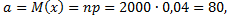
так как число бракованных деталей имеет биномиальное распределение. Оценим вероятность

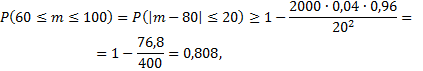
т.е. не менее 80%.

Применяя теорему Муавра-Лапласа, получим

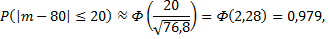
т.е.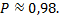

Различие результатов объясняется тем, что неравенство Чебышева дает лишь нижнюю границу оценки вероятности искомого события для любой случайной величины, а теорема Муавра-Лапласа дает достаточно точное значение самой вероятности 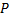(тем точнее, чем больше 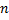), так как она применима лишь для случайной величины, распределенной по биномиальному закону.

Контрольные вопросы

1. Чем объясняется то, что нормально распределенная случайная величина широко распространена на практике?

2. Что понимают под законом больших чисел?

3. Сформулировать теорему Ляпунова.

4. В чем сущность теоремы Чебышева?