Закон распределения непрерывной случайной величины. Равномерный закон распределения непрерывной случайной величины
При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин.
Плотности распределения непрерывных случайных величин называют законами распределений.
Чаще всего встречаются законы равномерного, нормального и показательного распределений.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Пример равномерно распределенной непрерывной случайной величины: шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину 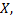 которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом,
которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом,  имеет равномерное распределение.
имеет равномерное распределение.
Найдем плотность равномерного распределения 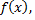 считая, что все возможные значения случайной величины заключены в интервале
считая, что все возможные значения случайной величины заключены в интервале 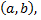 на котором функция
на котором функция  сохраняет постоянное значение
сохраняет постоянное значение

если 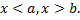
Должно выполняться соотношение
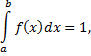
или
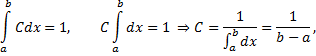
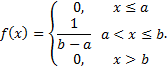
График функции будет выглядеть следующим образом (рис. 75).

Рис. 75
Плотность равномерного распределения
Вероятность попадания случайной величины  в интервале
в интервале 
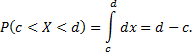
Функция распределения случайной величины 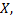 распределенной по равномерному закону, есть
распределенной по равномерному закону, есть

Ее математическое ожидание

дисперсия
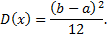
Покажем, как получились данные формулы.

При 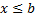
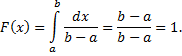
При 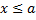

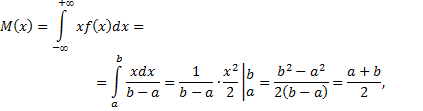
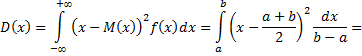

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, ошибка округления числа до целого распределена на отрезке 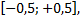 в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненных равномерному закону распределения.
в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненных равномерному закону распределения.
Рассмотрим пример. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше половины минуты. Найти  случайной величины
случайной величины 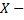 времени ожидания поезда.
времени ожидания поезда.
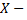 время ожидания поезда на временном отрезке
время ожидания поезда на временном отрезке 
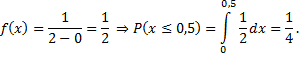
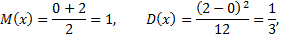

Дата добавления: 2015-08-11; просмотров: 1776;
