Закон распределения дискретной случайной величины. Биномиальное распределение дискретной случайной величины

Для задания дискретной случайной величины необходимо перечислить все ее возможные значения и указать вероятности их появления.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Закон распределения можно задать таблично, аналитически (в виде формулы) и графически.

Пусть производится независимых испытаний, в каждом из которых событие может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна 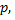следовательно, вероятность не появления 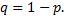Рассмотрим в качестве дискретной случайной величины число появлений события в этих испытаниях.

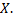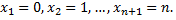Найдем закон распределения случайной величины Для решения поставленной задачи требуется определить возможные значения и их вероятности. Событие в независимых испытаниях может либо появиться, либо не появиться 1 раз, либо 2 раза, либо раз. Таким образом, возможные значения будут следующими: Остается найти вероятности этих возможных значений, для чего следует пользоваться формулой Бернулли

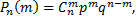
где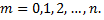

Данная формула является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли.

Биномиальный закон можно записать в виде таблицы.

Таблица 10

			…		…
			…		…

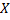
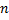
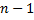
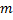
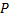
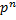
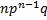
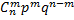
Пусть производится независимых испытаний, в каждом из которых вероятность появления события равна 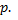Для определения вероятности появлений события в этих испытаниях используют формулу Бернулли. Если же велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала 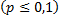. В этих случаях прибегают к асимптотической формуле Пуассона.