Дискретные и непрерывные случайные величины

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Например, число родившихся мальчиков среди 100 новорожденных.

Случайные величины обозначают заглавными буквами: X,Y,…

Их возможные значения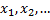

Целесообразно различать случайные величины, принимающие отдельные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому для задания дискретной случайной величины нужно указать все ее возможные значения и их вероятности.

46.2. Формы задания законов распределения случайных величин: ряд распределения, функция распределения, плотность распределения

Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями. Закон можно задать таблицей, аналитически или графически.

Таблично дискретная случайная величина задается следующим образом (табл. 9)

Таблица 9

			….
			….

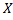
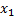
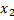
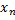
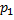
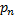
Данные события образуют полную группу, следовательно, сумма вероятностей этих событий равна единице

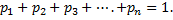
Рассмотрим пример. Возможные значения случайной величины таковы: 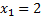, 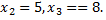Известны вероятности первых двух возможных значений: 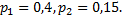Найти вероятность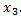

Зададим случайную величину в виде таблицы:

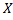
	0,4	0,15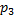

Так как данные события образуют полную группу, сумма вероятностей этих событий равна единице, следовательно, искомую вероятность следует найти по формуле

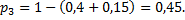
Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат отмечают точки 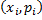, а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. При построении многоугольника распределения следует помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения, точки соединены только для наглядности.

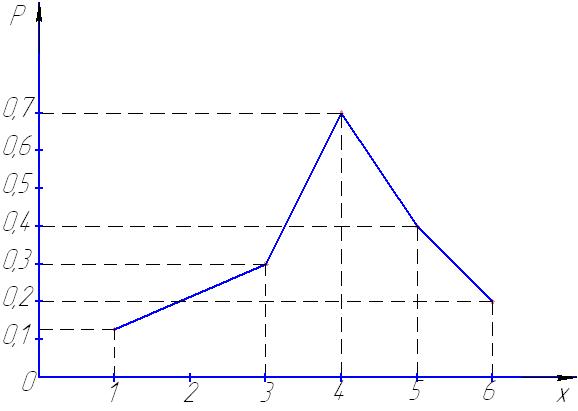
Рис. 72

Таким образом, дискретная случайная величина может быть задана перечнем всех возможных значений и их вероятностей. Такой способ задания не является общим, он неприменим для непрерывных случайных величин. Рассмотрим случайную величину 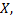возможные значения которой сплошь заполняют интервал 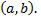В данном случае нет возможности составить перечень всех возможных значений 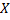. Существует более общий способ задания любых типов случайных величин – с помощью функции распределения вероятностей случайной величины.

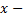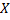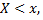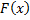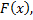Пусть действительное число. Вероятность события, состоящего в том, что примет значение, меньшее , т.е. вероятность события обозначим через . Если изменяется , то изменяется и т.е. 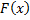- функция от переменной

Функцией распределения вероятностей называют функцию 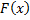, определяющую вероятность того, что случайная величина 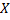в результате испытания примет значение, меньшее т.е.

Более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно– дифференцируемая функция с непрерывной производной.

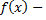Непрерывную случайную величину можно также задать, используя функцию плотности распределения вероятностей. Плотностью распределения вероятностей непрерывной случайной величины называют функцию первую производную от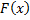

.

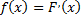Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.