Теоремы сложения вероятностей.
Теорема 1. Вероятность суммы двух несовместных событий А и В равна сумме их вероятностей:
P(A+B)=P(A)+P(B). (1.10)
Следствие 1. Если 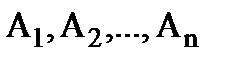 - попарно несовместные события, то вероятность их суммы равна сумме вероятностей этих событий:
- попарно несовместные события, то вероятность их суммы равна сумме вероятностей этих событий:
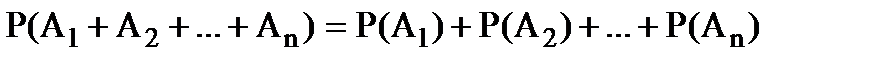 . (1.11)
. (1.11)
Следствие 2. Вероятность суммы попарно несовместных событий 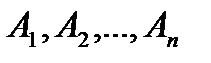 , образующих полную группу, равна 1:
, образующих полную группу, равна 1:
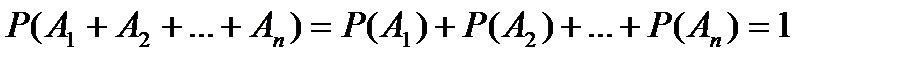 . (1.12)
. (1.12)
Следствие 3. События А и 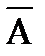 несовместны и образуют полную группу событий, поэтому
несовместны и образуют полную группу событий, поэтому
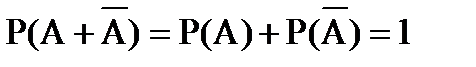 . (1.13)
. (1.13)
Отсюда,
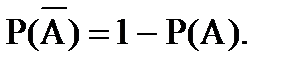
Теорема 2. Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их произведения:
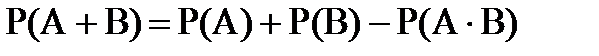 . (1.14)
. (1.14)
Введем понятие зависимых и независимых событий.
Два события А и В называются независимыми, если появление одного из них не влияет на вероятность появления другого (в противном случае события зависимы).
Теорема 3. Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:
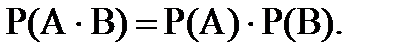 (1.15)
(1.15)
Следствие. Вероятность произведения n независимых событий 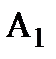 ,
, 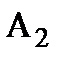 ,...,
,..., 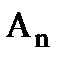 равна произведению их вероятностей:
равна произведению их вероятностей:
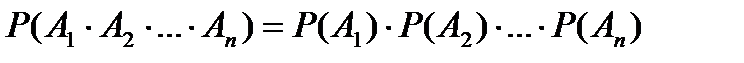 . (1.16)
. (1.16)
Условной вероятностью события В, при условии, что событие А уже произошло, называется число P(AB)/P(A), которое обозначается
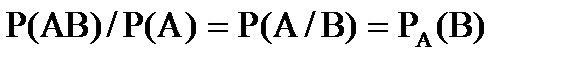 .
.
Аналогично, 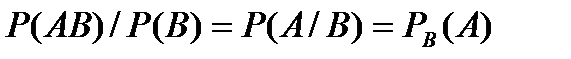 - условная вероятность события А, при условии, что событие В уже произошло.
- условная вероятность события А, при условии, что событие В уже произошло.
Теорема 4. Вероятность произведения 2-х зависимых событий А и В равна произведению вероятности наступления события А на условную вероятность события В при условии, что событие А уже произошло:
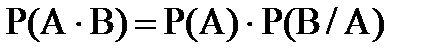 . (1.17)
. (1.17)
Следствие. Если события А и В независимы, то из теоремы 4 следует теорема 3.
Событие В не зависит от события А, если P(B/A)=P(B).
Теорема 5. Вероятность произведения n зависимых событий - 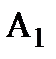 ,
, 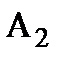 ,...,
,..., 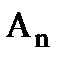 равна произведению последовательных условных вероятностей:
равна произведению последовательных условных вероятностей:
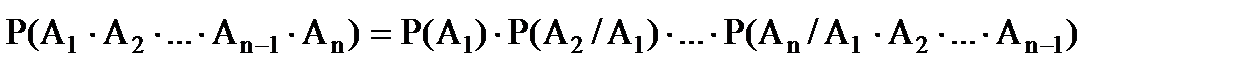 .(1.18)
.(1.18)
Теорема 6. Вероятность наступления хотя бы одного из событий А1, А2,…, Аn равна разности между единицей и вероятностью произведения отрицаний событий А1, А2,…, Аn:
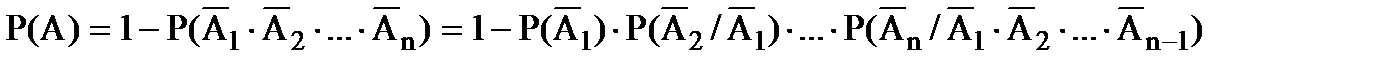 . (1.19)
. (1.19)
Следствие 1. Вероятность наступления хотя бы одного из событий 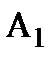 ,
, 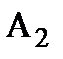 , ... ,
, ... , 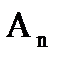 , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:
, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:
P(A)=1-P( 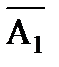 )·P(
)·P( 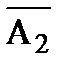 )·...·P(
)·...·P( 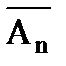 ). (1.20)
). (1.20)
Следствие 2. Если события имеют одинаковую вероятность появиться (P( 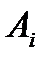 )=р, P(
)=р, P( 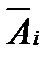 )=1-р=q, где i=1, 2,…, n), то вероятность появления хотя бы одного из них равна
)=1-р=q, где i=1, 2,…, n), то вероятность появления хотя бы одного из них равна
 (1.21)
(1.21)
Замечание. В теоремах 1-6 неявно предполагается, что все события, в рамках каждой теоремы, принадлежат одному пространству элементарных событий.
Дата добавления: 2015-08-11; просмотров: 670;
