Виды дисперсий. Правило сложения дисперсий
Вариация признаков в совокупности складывается под влиянием различных внешних и внутренних причин и факторов. Влияние некоторых из этих факторов можно изучить, проведя группировку совокупности по этому фактору. По проведенной группировке рассчитываются различные виды дисперсий:
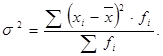 |
1 Общая дисперсия – характеризует всю вариацию, складывающуюся под влиянием всех факторов.
2 Межгрупповая дисперсия – характеризует вариацию, складывающуюся под влиянием только группировочного признака.
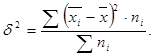 |
где x–общая средняя для всей совокупности;
x i – групповые средние;
n i – количество единиц в группах.
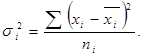 |
3 Внутригрупповая дисперсия – характеризует вариацию, складывающуюся под влиянием всех других факторов, кроме группировочного. Их будет столько, сколько групп в проведенной группировке.
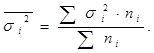 |
Средняя из внутригрупповых дисперсий.
Правило сложения дисперсий.
_
σ 2 = d 2 + σ i2.
Общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий.
Эмпирический коэффициент детерминации и корреляционное отношение
Сравнение различных видов дисперсий позволяет изучить влияние группировочного фактора на вариацию изучаемого показателя. Для этого применяют эмпирический коэффициент детерминации ŋ2 .
ŋ2 = d2 / σ 2 · 100 .
Чем больше доля межгрупповой дисперсии в общей, тем сильнее влияние группировочного фактора на общую вариацию.
Для изучения тесноты взаимосвязи между группировочным фактором и результативным признаком, рассчитанным по группам (в результате аналитической группировки), применяется эмпирическое корреляционное отношение ŋ.
_______
ŋ = √ ŋ2 / 100 , где 0≤ŋ ≤1.
Для того, чтобы сделать вывод по значению ŋ о тесноте взаимосвязи используются соотношения Чэддока.
| Ŋ | <0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 | |
| Теснота связи | Слабая | Умеренная | Заметная | Тесная | Очень тесная | Функциональная |
Дляŋ<0,1 – нет связи.
Тема: «Выборочный метод сбора данных».
1. Понятие выборочного метода, его преимущества.
2. Принципы выборочного метода, ошибки выборки.
3. Виды методы и способы отбора единиц в выборку.
4. Средняя ошибка выборки, способы ее расчета для различных выборок.
5. Предельная ошибка выборки.
6. Распространение результатов выборки.
Дата добавления: 2015-08-14; просмотров: 1039;
