Показатели вариации
Для оценки вариации в статистике применяют следующую систему показателей.
Абсолютные показатели:
1) размах вариации (R);
2) среднее линейное отклонение (ē);
3) дисперсия (σ2);
4) среднее квадратическое отклонение – СКО (σ).
Относительные показатели:
1) коэффициент осцилляции (VR);
2) коэффициент вариации (Vδ).
1. Размах вариации — это различие между крайними значениями признака
R= Xmax-Xmin
Недостатки:
1) не учитывает повторяемость значения признака;
2) если крайние значения являются аномальными, то размах не дает истинной картины вариации значений.
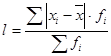 |
2. Среднее линейное отклонение — среднее абсолютное отклонение, используется при анализе ритмичности производства, равномерности поставок товаров, изучении состава работников и т. д.
3. Общепринятым показателем вариации является дисперсия.
Дисперсия— это средний квадрат отклонений индивидуальных значений от своей средней. Она не имеет единиц измерения.
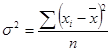 |
Простая дисперсия:
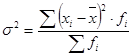 |
Взвешенная дисперсия:
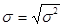 |
4. Среднеквадратическое отклонение– это корень квадратный из дисперсии (СКО), оно характеризует средний разброс индивидуальных значений вокруг своей средней.
СКО имеет те же единицы измерения, что и признак.
5. Коэффициент осцилляции — он характеризует максимальную степень разброса индивидуальных значений вокруг средней.
VR=R/xср.•100%
6. Коэффициент вариации — он характеризует среднюю степень разброса индивидуальных значений вокруг средней.
Vδ=σ /xср.•100%
Относительные показатели (VR, Vδ ) используются для сравнения вариаций по различным совокупностям или по одной совокупности за разное время. Vδиспользуется также для характеристики однородности совокупности по данному признаку.
Vδ < 33%- совокупность однородная
Vδ≥ 33%- совокупность неоднородная
3. Свойства σ 2 и σ, формулы их расчета.
Свойства:
1) Дисперсия и СКОσ 2 и σ– постоянной величины = 0.
2) Если все значения признака (xi) уменьшить или увеличить на число а, то дисперсия и СКО σ 2 и σ не изменятся.
3) Если все значения признака (xi) умножить или разделить на число k, то σ 2 изменится в k2 раз, а σ – в k раз.
 |
Упрощенная формула расчета дисперсии и СКО:
Используя свойства дисперсии и СКО, можно найти дисперсию признака в интервальных рядах распределения методом моментов:
1) находим середины интервалов xi;
2)
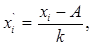 |
преобразуем данные
где А – середина интервала с наибольшей частотой,
k – ширина интервала;
3)
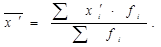 |
определяем среднюю для преобразованных данных по формуле (1).
4) определяем начальную дисперсию по преобразованной формуле и свойству 3.
 |
Для нормального закона распределения для показателей вариации существует взаимосвязь.
R≈ 6 · σ σ =1,25· l
Правило трех сигм для нормального закона распределения показывает, что в интервал(x – 3σ, x+ 3σ) попадает 99,7% всех индивидуальных значений xi.
Дата добавления: 2015-08-14; просмотров: 1318;
