Свойства средней арифметической

1. Произведение средней на объем совокупности равно сумме произведений индивидуальных значений признака на частоту.

2. Сумма отклонений индивидуальных значений признака от средней величины равна 0

3. Если все частоты f_i умножить или разделить на какое либо число А, то средняя не изменится.

4. Если все варианты Х_i умножить или разделить на какое либо число k, то средняя соответственно изменится в k раз.

5. Если все варианты увеличить или уменьшить на число А, то средняя соответственно увеличится или уменьшится на число А.

Свойства 4-5 позволяют рассчитывать среднюю арифметическую по интервальным ряда распределения методом моментов. Этот метод применяется для упрощения вычислений.

Метод моментов расчета средней величины.

1. Определяется середина интервалов x_i как средина отрезка. При этом ширина открытых интервалов (первого и последнего) считается равной ширине последующего или предыдущего.

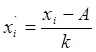2. Преобразуются исходные данные следующим образом:

где x_í – преобразованные данные;

x_i – исходные данные;

А – середина интервала с наибольшей частотой;

k – ширина интервала.

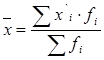3. Определяется средняя для преобразованных данных по формуле арифметической взвешенной.

4. Возвращаются обратно к исходной средней методом моментов:

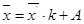Пример: Имеются данные распределения домохозяйств по уровню среднедушевого дохода. Результаты обследования представлены в таблице 1.

Таблица 1

Среднедушевой доход , руб.	До 200	200 -400	400 –600	600 –800	800 - 1000	1000 - 1200	1200 и более	Итого
Число домохозяйств

Определить средний стаж работников

Решение: Для расчетов построим расчетную таблицу 2.

Таблица 2

Среднедушевой доход, руб.	Число домохозяйств f_i	Середина x_i	x_í = (x_i– A)/k = = (x_i– 900)/200	x_í *f_i
До 200			-4	-20
200-400			-3	-36
400-600			-2	-48
600-800			-1	-56
800-1000		900 (A)
1000-1200
1200 и более
Итого		-	-	-129

Средняя для преобразованных данных равна

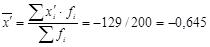Средняя для исходных данных равна

4. Средняя гармоническая. Другие виды средних.

Средняя гармоническая (взвешенная) применяется в тех случаях, когда известен числитель логической формулы средней и неизвестен знаменатель. Знаменатель можно найти как частное двух показателей.

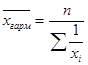где w_i = x_i*f_i. Если w_i одинаково у всех единиц совокупности, то для расчета средней применяется средняя гармоническая простая.

Пример 2. Известны данные по фирме о выпуске экспортной продукции за год (таблица 4).

Таблица 4

Вид продукции	Стоимость продукции на экспорт, тыс. руб.	Удельный вес продукции на экспорт от всей продукции, %	Стоимость всей продукции, тыс. руб.
w_i	x_i	W_i/ x_i*100
Сталь
Прокат
Итого		-

Определите средний удельный вес продукции на экспорт по предприятию.

Решение: Составим логическую формулу средней величины (экономическое содержание).

Средний удельный вес Стоимость продукции на экспорт

продукции на экспорт = _______________________________ * 100 .

Стоимость всей продукции

Так как по исходным данным известен числитель логической формулы и не известен знаменатель, то для расчетов данной средней величины будем применять среднюю гармоническую взвешенную. Неизвестные данные рассчитаем в таблице 4.

Таким образом, средний удельный вес экспортной продукции предприятия составляет 37%.

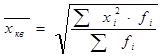Средняя квадратическая применяется для определения средней по показателям, имеющим квадратные единицы измерения, а также для расчета показателей вариации. Расчетная формула имеет вид:

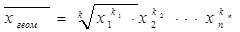Средняя геометрическая применяется для определения средних темпов роста в рядах динамики. При этом варианты x_i представляют собой цепные относительные показатели динамики,

где k = k₁+ k₂ +….+ k_n .

5. Структурные средние.

Структурные средние применяются для характеристики рядов распределения. К ним относятся мода и медиана.

Мода (М_о) – это наиболее часто встречающееся значение признака в совокупности, т.е. значение, имеющее наибольшую частоту.

Медиана (Ме) – это середина ряда распределения, т.е. значение признака, делящее рад распределения пополам по количеству единиц совокупности. Половина единиц совокупности имеют значения признака меньше медианы, вторая половина больше медианы.

Для нахождения моды по дискретному ряду распределения нужно выбрать значение, имеющее наибольшую частоту. Моды могут быть одна или две.

Для нахождения медианы по дискретному ряду распределения необходимо определить накопленные частоты и найти номер середины ряда. Далее выбирается то значение признака, где превышается половина единиц совокупности, т.е. значение из той группы единиц, в которой находится середина ряда распределения.

Мода и медиана по интервальным рядам с равными интервалами определяется по формулам.

Где Xм_о – нижний конец модального интервала (с наибольшей частотой);

k – ширина интервала;

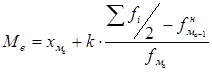f_Мо, f_Мо-1, f_Мо+1– частоты в модальном интервале, до него и после него.

Медиана определяется по формуле

Где X_Ме– нижний конец медианного интервала (где превышена половина единиц совокупности по накопленным частотам);

k – ширина интервала;

f_Ме– частота в медианном интервале;

f_Ме-1^Н – накопленная частота до модального интервала.

Соотношение средней, моды и медианы между собой позволяет сделать вывод об асимметрии распределения признака в совокупности.

1. Распределение симметрично, если

2. Распределение имеет правостороннюю асимметрию, если

3. Распределение имеет левостороннюю асимметрию, если

Тема: «Показатели вариации».

1. Понятие вариации, ее виды.

2. Показатели вариации.

3. Свойства дисперсии, формулы ее расчета.

4. Вариация альтернативного признака.

5. Виды дисперсий, правило сложения дисперсий, коэффициент детерминации, эмпирическое корреляционное отношение.

<10 11 121314 15 16 >

Дата добавления: 2015-08-14; просмотров: 803;