ГЛАВА 7. Теоремы о среднем
8.1. Теорема Ферма[13]
| Т. | (Теорема Ферма) Пусть функция y=f(x) определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда, если в т. 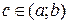 функция достигает локального экстремума, то функция достигает локального экстремума, то 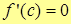 . .
|
| Note 1 | Локальным экстремумом называют локальный («местный») максимум или минимум. |
Proof:
Пусть в т. 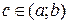 функция y=f(x) достигает локального максимума.
функция y=f(x) достигает локального максимума.

По определению производной 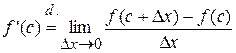 .
.
| Note 2 | Приращение аргумента может быть любым, т.е. 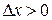 или или 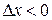 . .
|
1. Пусть 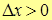
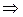
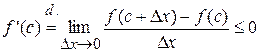 , т.к. числитель имеет знак «-», а знаменатель знак «+».
, т.к. числитель имеет знак «-», а знаменатель знак «+».
2. Пусть 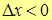
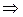
 , т.к. числитель имеет знак «-», и знаменатель знак «-».
, т.к. числитель имеет знак «-», и знаменатель знак «-».
| Note 3 | f '(c) – значение производной в т. с. Это значение не может быть одновременно меньше или больше нуля. Т.о. f '(c) =0, ч. т. д. |
8.2. Теорема Ролля[14]
| Т. | (Теорема Ролля) Пусть функция y=f(x) определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда, если на концах отрезка функция принимает равные значения f(a)=f(b), то 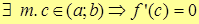 . .
|
Proof:
По второй теореме Вейерштрасса – функция, непрерывная на отрезке, достигает своего максимального М и минимального m значения.
Возможны два варианта:
1. Пусть М=m на [a;b] 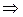 функция
функция 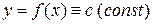 .
.
Тогда в 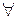 т.
т. 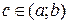
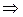
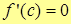 , ч.т.д.
, ч.т.д.
2. Пусть 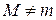 , тогда по теореме Ферма (п.7.1.)
, тогда по теореме Ферма (п.7.1.) 
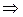
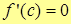 , ч.т.д.
, ч.т.д.
7.3. Теорема Лагранжа[15]. Геометрический смысл
| Т. | (Теорема Лагранжа) Пусть функция y=f(x) определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда, 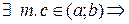 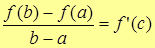 . .
|
Proof:
Чтобы воспользоваться теоремой Роля (п.7.2.) введем вспомогательную функцию
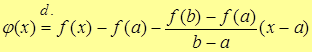 .
.
Очевидно, что 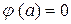 и
и 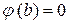 , тогда по теореме Роля
, тогда по теореме Роля 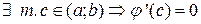 .
.
Но, производная 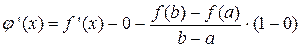 .
.
В т. 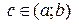 производная
производная 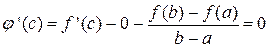 (по теореме Ролля).
(по теореме Ролля).
Или 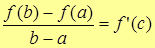 , ч.т.д.
, ч.т.д.
Геометрический смысл
Очевидно, что 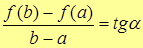 – тангенс угла «наклона» хорды, соединяющей точки
– тангенс угла «наклона» хорды, соединяющей точки 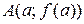 и
и 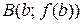 к оси ОХ.
к оси ОХ.
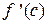 – угловой коэффициент касательной к графику функции в т.
– угловой коэффициент касательной к графику функции в т. 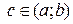 .
.
| Note | Таким образом, тангенс угла «наклона» хорды равен угловому коэффициенту касательной в т. 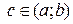 . .
|

Дата добавления: 2015-08-20; просмотров: 1105;
