Признаки возрастания и убывания функции

Пусть функция y=f(x) определена и дифференцируема в некоторой области т.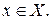

Т.1	(Прямая) Если функция y=f(x) возрастает (в строгом смысле) на множестве X, то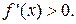

Proof:

Пусть 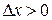, тогда .

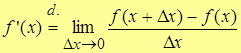По условию теоремы 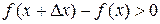, т.к. функция возрастает; 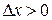по предположению, значит 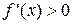, ч.т.д.

Note 1

Дома или на практическом занятии доказать, что если функция y=f(x) убывает (в строгом смысле) на множестве Х, то .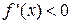

Т.2	(Обратная) Если на множестве X 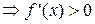, то функция y=f(x) возрастает (в строгом смысле).

Proof:

Пусть 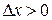, тогда по теореме Лагранжа 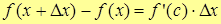, где . Так как правая часть строго больше нуля, то и левая часть больше нуля, т.е. 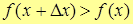, ч.т.д.

Note 2

Дома или на практическом занятии доказать, что если на множестве X 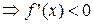, то функция y=f(x) убывает (в строгом смысле).