Общая схема исследования функции и построение ее графика. Пусть задана функция y=f(x) в д.п.с.к
Пусть задана функция y=f(x) в д.п.с.к. X0Y.
Общая схема
1. D [f(x)] – область определения функции (О.О.Ф.)
2. E [f(x)] – область значений функции (О.З.Ф.)
3. Нули функции, чётность, нечётность, периодичность.
4. 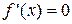 – точки локального экстремума.
– точки локального экстремума.
5. 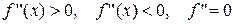 с – вогнутость, выпуклость и точки перегиба.
с – вогнутость, выпуклость и точки перегиба.
6. Вертикальные и наклонные асимптоты.
7. Заполнение таблицы.
| Note 1 | В первую строку таблицы заполняется О.О.Ф., которая делится на промежутки точками разрыва 1-го и 2-го рода и другими характерными точками. |
| Note 2 | Заполнение таблицы начинают с производной  . .
|
| Note 3 | Для «простых» функций таблицу можно не формировать. |
| Note 4 | Построение графика функции начинают с асимптот, которые наносятся пунктиром. |
Ex. 1. Исследовать функцию 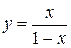 и построить ее график.
и построить ее график.
Решение
1. 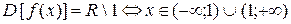 . В т. x=1 функция имеет разрыв 2-го рода (x=1 – вертикальная асимптота).
. В т. x=1 функция имеет разрыв 2-го рода (x=1 – вертикальная асимптота).
2. 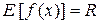 (значение функции не ограничено, однако точное значение функции можно получить, выразив x=x(y), т.е.
(значение функции не ограничено, однако точное значение функции можно получить, выразив x=x(y), т.е. 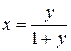 , т.е. более точное значение
, т.е. более точное значение 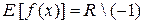 .
.
3. Нули функции. 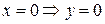 . Функция не является ни чётной, ни нечётной, ни периодической. Т.е. функция общего вида.
. Функция не является ни чётной, ни нечётной, ни периодической. Т.е. функция общего вида.
4. 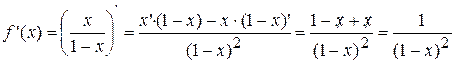 .
.
Т.о. 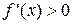 при всех x, кроме т. x=1.
при всех x, кроме т. x=1.

5. 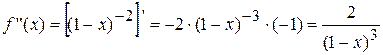 .
.

6. Асимптоты.
Вертикальная x=1.
Наклонная y=kx+b.
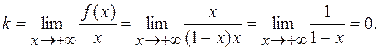
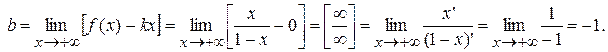
Т.о., k=0, b= -1.
Наклонная асимптота имеет уравнение y= -1.
7. Таблица.
| x | 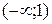
| 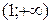
| |
| f(x) | 
| 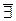
| 
|

| + | 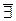
| + |
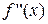
| + | 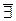
| - |
| Выводы | Возрастает вогнуто | Разрыв 2-го рода | Возрастает выпукло |


График функции 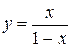 .
.
[1] Leonard Euler (1707-1783) – швейц. математик, механик, физик, астроном. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, физике, оптике, баллистике, кораблестроению, теории музыки и др. Член Петерб. АН (с 1766 г.).
D. Venn (1834-1923) – англ. математик, логик. Труды по логике классов, теории вероятностей и индуктивной логике
[2] René Descartes (1596-1650) – франц. философ, математик, физик, физиолог. Труды по аналитической геометрии, теории функций, теории движения небесных тел, теории связи «души» человека с материей. Автор законов сохранения количества движения и импульса силы, …
[3] Augustin Louis Cauchy (1789-1857) – франц. математик, почетный член Пет. АН (1831). Труды по теории дифференциальных уравнений, математической физике, теории чисел, геометрии. Основоположник теории аналитических функций.
Виктор Буняковский (1804-1889) – русс. математик, академик Пет. АН (1830). Труды по интегральному исчислению, теории вероятностей, теории чисел, статистике населения.
[4] Фалес – ок. 625 г. до н.Э., др. греч. мыслитель, родоначальник антич. философии и науки, основатель милетской школы. Возводил все многообразие явлений и вещей к единой первостихии – воде.]
[5]Пифагор Самосский (6 в. до н.э.) – др. греч. философ, математик. Труды по теории целых чисел, пропорций,….
[6] Isaak Newton (1643-1727) – англ. математик, механик, астроном и физик. Фунд. труд «Математические начала натуральной философии» (1687).
[7] Gottfried Willhelm Leibniz (1646-1716) – нем. философ-идеалист, математик, физик, языковед. Основатель Бранденбургского науч. общества. По просьбе Петра 1 разработал проекты развития образования и государственного управления России.
[8] Heine (1821-1881) – нем. математик
[9] Augustin Louis Cauchy (1789-1857) – франц. математик, основоположник теории аналитических функций. Тр. по теории дифференциальных уравнения, математической физике, теории чисел, геометрии. Автор классических курсов математического анализа.
[10] [Bernhard Bolzano (1781-1848) – нем. математик и философ-идеалист. Истинам логики приписывал идеальное объективное существование. Тр. по математическому анализу, бесконечным множествам. Предшественник Г. Кантора].
[11] Karl Th. W. Weierstrass (1815-1897) – нем. математик. Тр. по математическому анализу, теории функций, вариационному исчислению, дифференциальной геометрии и линейной алгебре.
[12] Georg Cantor (1845-1918) – нем. математик. Разработал основы теории множеств, оказавшей большое влияние на развитие всей математики.
[13] Pierre de Fermat (1601-1665) – гениальный франц. математик. Труды по аналитической геометрии, теории чисел, теории вероятностей, оптике, …
[14] Michele Rolle (1652-1715) – франц. математик. Труды по алгебраически уравнениям, …
[15] Joseph Louis de Lagrange (1736-1813) - франц. математик, механик, физик,… Труды по вариационному исчислению, теории чисел, алгебре, дифференциальным уравнениям, …
[16] Augustin Louis Cauchy (1789-1857) - франц. математик, почетный член пет. АН (1831). Труды по теории дифференциальных уравнений, математической физике, теории чисел, геометрии. Основоположник теории аналитических функций.
[17] Guillaumede L’Hospital (1661-1704) – франц. математик. Первый печатный учебник по дифференциальному исчислению (1696).
[18] Brook Tailor (1685-1731) – англ. математик. Труды по степенным рядам.
[19] Colin Maclorin (1698-1746) – шотл. математик. Труды по математическому анализу, теории кривых, механике.
[20] D. Peano (1858-1932) – итал. математик. Труды по математическому анализу, теории чисел.
Дата добавления: 2015-08-20; просмотров: 931;
