Выпуклость и вогнутость графика функции
| Def.1 | График функции y=f(x) называется выпуклым в окрестности т. 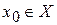 , если он находится «целиком» ниже касательной, проведенной в т. , если он находится «целиком» ниже касательной, проведенной в т. 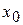 . .
|


Таким образом, если 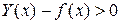 в окрестности т.
в окрестности т. 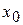 , то график функции y=f(x) – выпуклый.
, то график функции y=f(x) – выпуклый.
Причем: 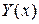 – ордината касательной в т.
– ордината касательной в т. 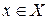 ;
;
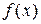 – ордината функции в т.
– ордината функции в т. 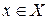 .
.
| Def.2 | График функции y=f(x) называется вогнутым в окрестности т. 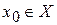 , если он находится «целиком» выше касательной, проведенной в т. , если он находится «целиком» выше касательной, проведенной в т. 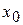 . .
|
| Т.1 | Пусть функция y=f(x) определена и дважды дифференцируема в окрестности т. 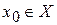 . Тогда, если в т. x0 :
1. . Тогда, если в т. x0 :
1. 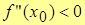 , то график функции выпуклый;
2. , то график функции выпуклый;
2. 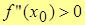 , то график функции вогнутый;
3. , то график функции вогнутый;
3. 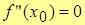 , то график функции имеет перегиб. , то график функции имеет перегиб.
|
Proof:
1. Пусть в т.  .
.
Рассмотрим отрезок [x0; x].
Уравнение касательной 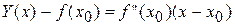 .
.
По теореме Лагранжа 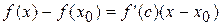 .
.
Вычтем из 2-го уравнения 1-е:
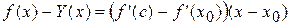 .
.
Применим для первого сомножителя правой части еще раз теорему Лагранжа
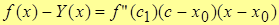 .
.
Учитывая знаки сомножителей в правой части:
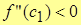 – по условию (в окрестности т. x0);
– по условию (в окрестности т. x0);
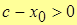 – по построению;
– по построению;
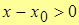 – по построению.
– по построению.
Тогда 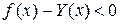 , т.е.
, т.е.
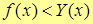 – ч.т.д.
– ч.т.д.
Т.е. график функции «целиком» лежит ниже касательной в окрестности т. 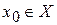 , т.е. он выпуклый, ч.т.д.
, т.е. он выпуклый, ч.т.д.
| Note | Дома или на практическом занятии аналогично доказать п.2 и п.3 . |
Дата добавления: 2015-08-20; просмотров: 1063;
