Формула конечных приращений
Если т. a=x, b=x+Δx 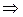 отрезок [x; x+Δx], то по теореме Лагранжа
отрезок [x; x+Δx], то по теореме Лагранжа
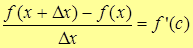 ,
,
где 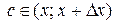 .
.
Или, учитывая, что 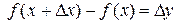 ,
, 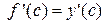 , получим
, получим
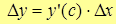 – формула конечных приращений.
– формула конечных приращений.
| Note |  Формула конечных приращений часто применяется в математике при различных доказательствах. Однако следует помнить, что где именно расположена точка с, теорема Лагранжа (к сожалению!) не дает ответа. Единственно, что следует из теоремы, это т. Формула конечных приращений часто применяется в математике при различных доказательствах. Однако следует помнить, что где именно расположена точка с, теорема Лагранжа (к сожалению!) не дает ответа. Единственно, что следует из теоремы, это т. 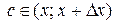 . .
|
7.4. Теорема Коши[16]
| Т. | (Теорема Коши) Пусть две функции f(x) и g(x) определены и непрерывны на отрезке [a;b] и дифференцируемы на интервале (a;b) и производная  на (a;b). Тогда, на (a;b). Тогда, 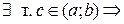 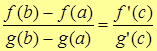 . .
|
Proof:
Чтобы воспользоваться теоремой Роля (см. п. 7.2) введем вспомогательную функцию
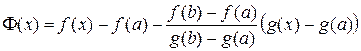 .
.
Очевидно, что 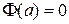 ,
, 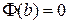 . Тогда по теореме Роля
. Тогда по теореме Роля 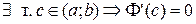 .
.
Производная
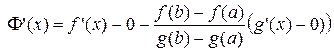 .
.
В т. 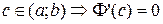 , т.е.
, т.е.
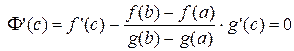 .
.
Откуда 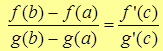 , ч.т.д.
, ч.т.д.
7.5. Правило Лопиталя[17]. Раскрытие неопределенностей
| Т. | (Теорема Лопиталя) Пусть две функции f(x) и g(x) определены и непрерывны на отрезке [x0; x] и дифференцируемы на интервале (x0; x), причем  . Пусть . Пусть  и и 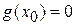 . Тогда, если существует . Тогда, если существует  то то 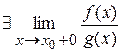 , причем , причем
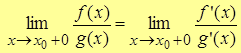 . .
|
Proof:
По теореме Коши 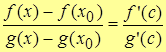 , где
, где 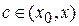 .
.
По условию теоремы 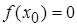 и
и 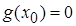 , т.е.
, т.е. 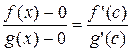 .
.
Тогда при 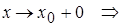 (по теореме о сжатой переменной)
(по теореме о сжатой переменной) 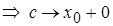 .
.

Или 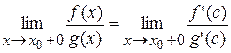 .
.
Пусть 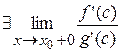 , тогда при
, тогда при 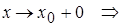
 , т.о. символ «с» можно заменить на символ «x», т.е. если
, т.о. символ «с» можно заменить на символ «x», т.е. если
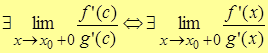 .
.
| Note 1 | Если рассмотреть отрезок [x; x0] и провести аналогичное доказательство, то все рассуждения справедливы при 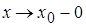 .
Поэтому в дальнейшем будем писать .
Поэтому в дальнейшем будем писать 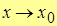 . .
|
| Note 2 | Пусть в т. 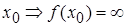 и и 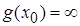 , тогда справедливы все выводы теоремы Лопиталя. , тогда справедливы все выводы теоремы Лопиталя.
|
| Note 3 | Т.о., если 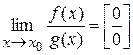 или или 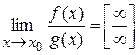 , то справедливо «Правило Лопиталя». , то справедливо «Правило Лопиталя».
|
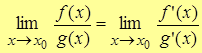 – Правило Лопиталя,
– Правило Лопиталя,
причем, следует иметь ввиду, что его необходимо читать «справа-налево», т.е. если существует предел отношения производных, то существует предел отношения функций и эти пределы совпадают.
Ex.1. 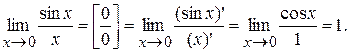
Ex.2. 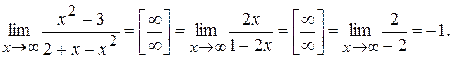
Ex.3. 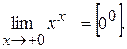
Пусть 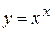 , тогда
, тогда 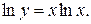
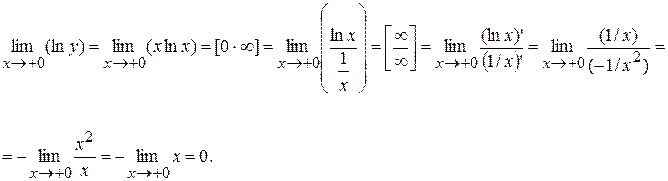
Т.о., 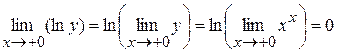 , откуда
, откуда
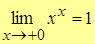 .
.
7.6. Многочлен Тейлора[18] и Маклорена[19]. Остаточный член в форме Пеано и Лагранжа
| Т. | Пусть функция y=f(x) определена и (n+1) раз дифференцируема в некоторой окрестности т. 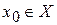 . Тогда справедлива формула Тейлора: . Тогда справедлива формула Тейлора: 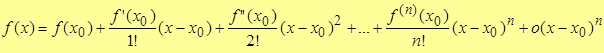 . Или более кратко . Или более кратко
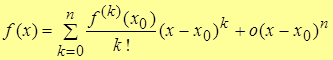 – формула Тейлора. – формула Тейлора.
|
Proof:
Пусть 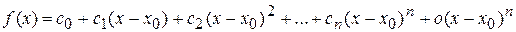 .
.
Пусть 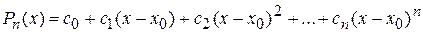 – многочлен n-й степени,
– многочлен n-й степени, 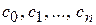 – неизвестные константы.
– неизвестные константы.
Тогда 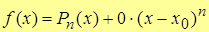 .
.
Пусть выполняется (n+1)-е условие:
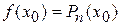 ,
,
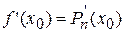 ,
,
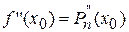 ,
,
………………..
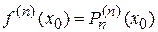 .
.
Напомним, что
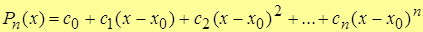 .
.
1. Пусть х=х0, тогда
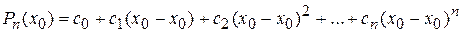
или
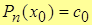
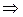
 .
.
Вычислим производную от многочлена Pn(x).
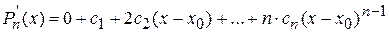 .
.
2. Пусть х=х0, тогда
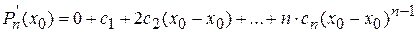
или
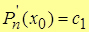
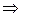
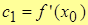
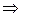
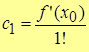 .
.
Вычислим производную 2-го порядка от Pn(x).
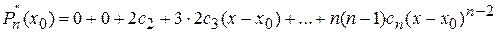 .
.
3. Пусть х=х0, тогда
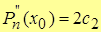
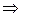
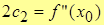
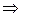
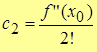 .
.
Продолжая этот процесс, вычисляя производные 3-го, 4-го, 5-го, …, n-го порядка, и, подставляя вместо 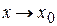 , получим
, получим
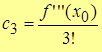 ,
, 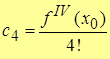 , …,
, …, 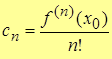 .
.
Подставляя эти значения констант в формулу для многочлена Pn(x), получим
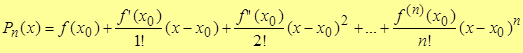 .
.
Докажем, что 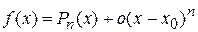
или
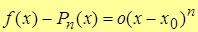 ,
,
т.е.
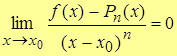 .
.
| Note 1 | Дома или на практическом занятии (применяя n раз правило Лопиталя) доказать, что
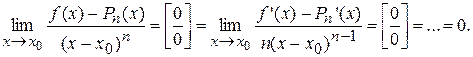
|
| Note 2 | Т.о. мы получили формулу Тейлора
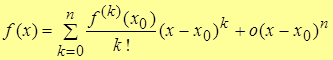 с остаточным членом
с остаточным членом 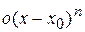 в форме Пеано[20]. в форме Пеано[20].
|
| Note 3 | Дома или на практическом занятии (применяя n+1 раз теорему Коши) доказать, что
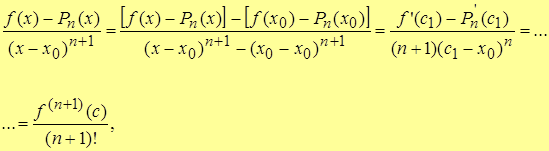 где
где 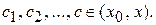
|
Т.о., 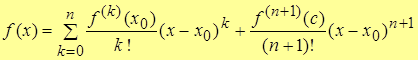 – формула Тейлора
– формула Тейлора
с остаточным членом 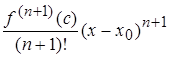 – в форме Лагранжа.
– в форме Лагранжа.
| Note 4 | Если в формуле Тейлора положить x0 = 0 !!!, то получим формулу Маклорена
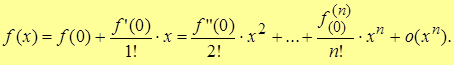 Или более кратко
Или более кратко
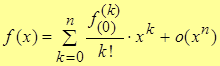 – формула Маклорена. – формула Маклорена.
|
| Note 5 | Дома или на практическом занятии получить формулы Маклорена для элементарных функций
1. 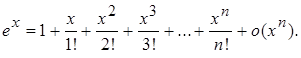 2.
2. 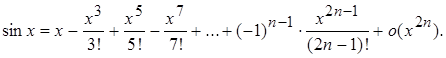 3.
3. 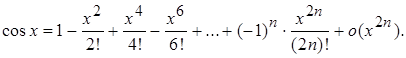 4.
4. 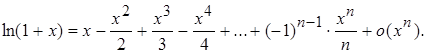 5.
5. 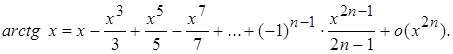
|
Дата добавления: 2015-08-20; просмотров: 1065;
