Дифференцирование неявной функции и функции, заданной параметрически
1. Дифференцирование функции, заданной неявно
Пусть функция y=y(x) задана неявно, т.е. F(x;y)=0 или F(x;y(x))=0.
Если функция F(x;y) – непрерывно дифференцируема в некоторой области D координатной плоскости X0Y, причем, частная производная функции двух переменных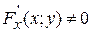 
, то можно доказать, что
.
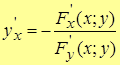Эта формула будет доказана далее в разделе «Функции нескольких переменных». Следует заметить, что переменные в функции F(x;y) считаются независимыми.
Однако не обязательно разрешать уравнение F(x;y)=0 относительно y. Достаточно продифференцировать это уравнение, считая y не переменной, а функцией аргумента x.
Ex. 1. Вычислить производную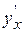 
, если уравнение задано неявно 
.
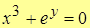Решение.
Продифференцируем это уравнение по переменной x, считая y=y(x), тогда получим
.
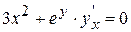Откуда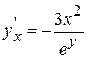 
или, учитывая (из заданного уравнения), что 
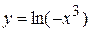, получим 
.
.
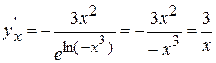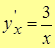2. Дифференцирование функции, заданной параметрически
Пусть функция y=y(x) задана параметрически, т.е.
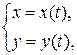где параметр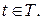 
По правилу дифференцирования сложной и обратной функции
.
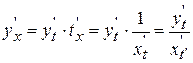Т.о.,
.
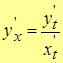Ex. 2. Найти производную 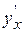, если функция задана параметрически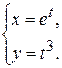 
Решение.
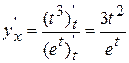, т.о.,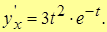 
Дата добавления: 2015-08-20; просмотров: 1065;