Производные и дифференциалы высших порядков. Пусть функция y=y(x) определена и дифференцируема в т
Пусть функция y=y(x) определена и дифференцируема в т. 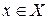 . Тогда
. Тогда 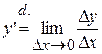 называют производной 1-го порядка. Т.к. производная 1-го порядка также является функцией, то ее можно дифференцировать.
называют производной 1-го порядка. Т.к. производная 1-го порядка также является функцией, то ее можно дифференцировать.
| Def. | Производной 2-го порядка называют производную от производной 1-го порядка, т.е.
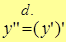 – производная 2-го порядка (по Лагранжу)
или – производная 2-го порядка (по Лагранжу)
или
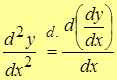 – производная 2-го порядка (по Лейбницу). – производная 2-го порядка (по Лейбницу).
|
Символ 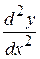 можно рассматривать как единый символ, который читается как «дэ два игрек по дэ икс дважды».
можно рассматривать как единый символ, который читается как «дэ два игрек по дэ икс дважды».
Однако, учитывая, что 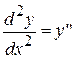 , то
, то 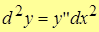 .
.
Т.о., мы получили формулу для вычисления дифференциала 2-го порядка, т.е. 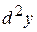 – дифференциал 2-го порядка.
– дифференциал 2-го порядка.
Аналогично вычисляются дифференциалы 3-го порядка 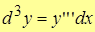 , 4-го порядка
, 4-го порядка 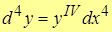 , и т.д.
, и т.д.
Ex.1. Вычислить дифференциал 3-го порядка для функции y=sinx.
Решение.
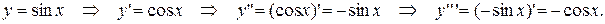
Т.о.,
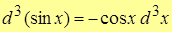 .
.
Дата добавления: 2015-08-20; просмотров: 936;
