Определение. Правила и формулы дифференцирования
Пусть на плоскости с д.п.с.к. X0Y определена функция y=f(x) в некоторой т. 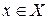 .
.
| Def.1 | (Наизусть!) Производной функции y=f(x) в т. x называют пределотношения приращения функции к приращению аргумента, когда последнее стремится к нулю, т.е.
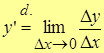 ,
где ,
где 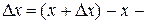 приращение аргумента; приращение аргумента;
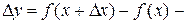 приращение функции. приращение функции.
|
| Note | Приращение аргумента 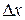 может быть как больше нуля, так и меньше нуля. может быть как больше нуля, так и меньше нуля.
|
| Def.2 | Функция y=f(x) называется дифференцируемой в т. х, если в этой точке существует конечная производная. |
Обозначение производной
y' или f '(x) – по Лагранжу;
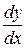 или
или 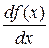 – по Лейбницу;
– по Лейбницу;
Dy или Df(x) – по Коши;
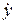 или
или 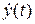 – по Ньютону.
– по Ньютону.
В данном курсе мы будем применять первые два типа обозначений (т.е. по Лагранжу или по Лейбницу), обозначение по Ньютону применяют в курсе «Теоретическая механика».
Основные правила и формулы дифференцирования
Правила
Пусть функции y=f(x), u=u(x), v=v(x) – определены и дифференцируемы в т. 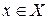 .
.
Пусть с – произвольная постоянная (с – const).
Пусть y=y[u(x)] – сложная функция от основного аргумента x (u(x) – называют промежуточным аргументом).
Тогда:
1. 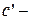 производная константы;
производная константы;
2. 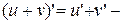 производная суммы функций;
производная суммы функций;
3. 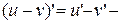 производная разности функций;
производная разности функций;
4. 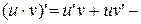 производная произведения функций;
производная произведения функций;
5. 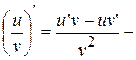 производная частного функций;
производная частного функций;
6. 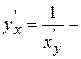 производная обратной функции;
производная обратной функции;
7. 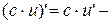 где с – const;
где с – const;
8. 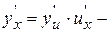 производная сложной функции.
производная сложной функции.
При выводе данных правил полагаем, что
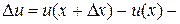 приращение функции u;
приращение функции u;
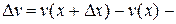 приращение функции v.
приращение функции v.
Формулы
Таблица производных элементарных функций
1. 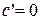
2. 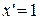
3. 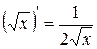
4. 
5. 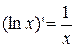
6. 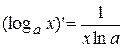
7. 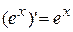
8. 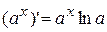
9. 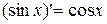
10. 
11. 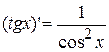
12. 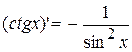
13. 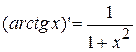
14. 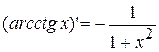
15. 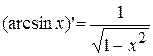
16. 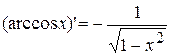
| Т. | (Связь между дифференцируемостью и непрерывностью функции) Если функция y=f(x) дифференцируема в т. x, то она непрерывна в т. х (обратное не всегда верно!). |
Proof:
1-й метод. Пусть 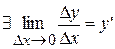 , тогда по лемме переменная
, тогда по лемме переменная 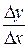 отличается от предела
отличается от предела 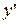 на б.м.в. α, т.е.
на б.м.в. α, т.е. 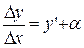 . Откуда
. Откуда 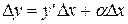 . Пусть
. Пусть 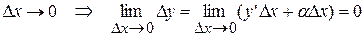 , ч.т.д.
, ч.т.д.
2-й метод. Пусть 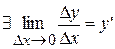 .
.
Тогда 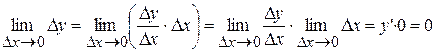 , ч.т.д.
, ч.т.д.
Мы воспользовались одним из определений непрерывности функции y=f(x)
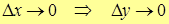 .
.
Правила
Proof:
1. 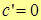 , т.е. производная константы равна нулю.
, т.е. производная константы равна нулю.
 Proof:
Proof:
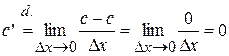 , ч.т.д.
, ч.т.д.
2. 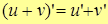 , т.е. производная суммы функций.
, т.е. производная суммы функций.
Proof:
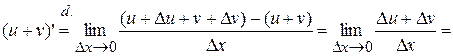
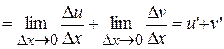 , ч.т.д.
, ч.т.д.
3. 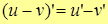 , т.е. производная разности функций.
, т.е. производная разности функций.
Proof:
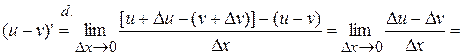
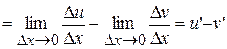 , ч.т.д.
, ч.т.д.
4. 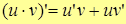 , т.е. производная произведения функций.
, т.е. производная произведения функций.
Proof:
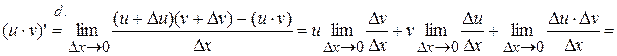
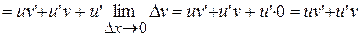 , ч.т.д.
, ч.т.д.
5. 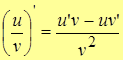 , т.е. производная частного функций.
, т.е. производная частного функций.
Proof:
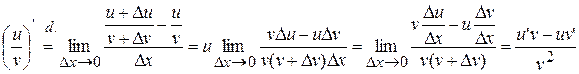 , ч.т.д.
, ч.т.д.
6. 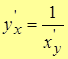 , т.е. производная обратной функции.
, т.е. производная обратной функции.
Proof:
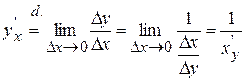 , ч.т.д.
, ч.т.д.
7. 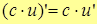 , где с – const.
, где с – const.
Proof:
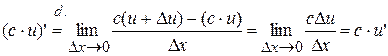 , ч.т.д.
, ч.т.д.
8. 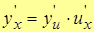 , т.е. производная сложной функции.
, т.е. производная сложной функции.
Proof:
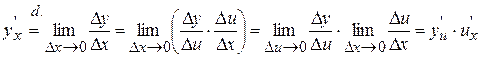 , ч.т.д.
, ч.т.д.
Формулы
Proof:
| Note | Приведем вывод некоторых формул, при этом нарушив их порядок. Остальные формулы вывести дома или на п/з. |
5. 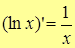 .
.
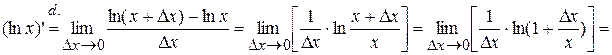

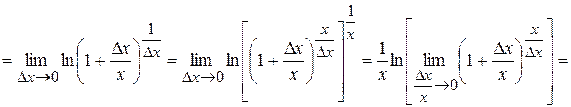
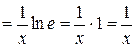 , ч.т.д.
, ч.т.д.
6. 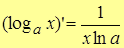 .
.
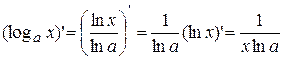 , ч.т.д.
, ч.т.д.
7. 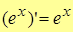 .
.
Пусть ex =y, тогда x=lny или 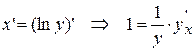 , (т.к. y – сложная функция переменной х). Или
, (т.к. y – сложная функция переменной х). Или 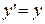 , т.е.
, т.е. 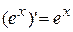 , ч.т.д.
, ч.т.д.
8. 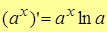 .
.
Пусть 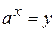 , тогда
, тогда 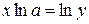 , или
, или 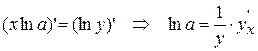 (т.к. y – сложная функция переменной х). Или
(т.к. y – сложная функция переменной х). Или 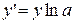 , т.е.
, т.е. 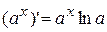 , ч.т.д.
, ч.т.д.
4. 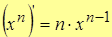 .
.
Пусть 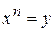 , тогда
, тогда 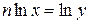 или
или 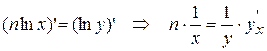 (т.к. y – сложная функция переменной x).
(т.к. y – сложная функция переменной x).
Или 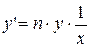 , т.е.
, т.е. 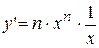 ,
, 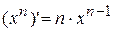 , ч.т.д.
, ч.т.д.
9. 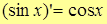 .
.
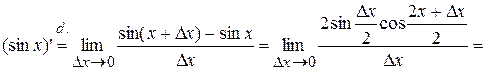
 , ч.т.д.
, ч.т.д.

10. 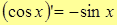 .
.
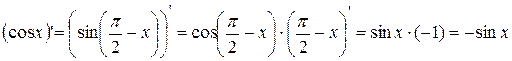 , ч.т.д.
, ч.т.д.
15. 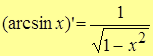 .
.
Пусть 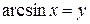 , тогда
, тогда 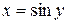 , или, учитывая, что
, или, учитывая, что 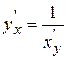 , т.е.
, т.е.
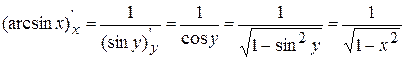 , т.е.
, т.е. 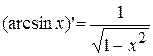 , ч.т.д.
, ч.т.д.
| Note | Т.к. 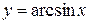 монотонно возрастает на монотонно возрастает на 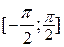 , то в последней формуле перед радикалом выбираем знак «+». , то в последней формуле перед радикалом выбираем знак «+».
|
Дифференциал. Инвариантность формы записи дифференциала
Пусть функция y=f(x) определена и дифференцируема в т. 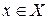 , т.е.
, т.е. 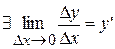 , это значит, что переменная
, это значит, что переменная 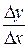 отличается от предела y’ на б.м.в. (при
отличается от предела y’ на б.м.в. (при  ).
).
Т.е. 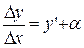 или
или 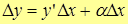 – приращение функции.
– приращение функции.
Если 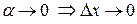 .
.
Произведение двух б.м.в. есть б.м.в. более высокого порядка малости, чем 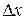 , т.е.
, т.е. 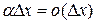 .
.
Т.о. 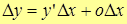 .
.
Более того, б.м.в. 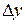 и
и 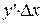 эквиваленты, т.е. предел их отношения равен единице, т.е.
эквиваленты, т.е. предел их отношения равен единице, т.е.
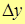 ~
~ 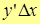 .
.
| Note 1 | В приближенных методах вычисления используется запись
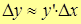 . .
|
| Т. | Если две б.м.в. эквиваленты, то каждая из них является главной частью другой.
Т.е. если α ~ β (  при при  ), то ), то
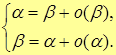
|
Proof:
Пусть α ~ β 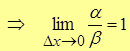 , тогда по лемме переменная
, тогда по лемме переменная 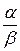 отличается от предела 1 на б.м.в., т.е.
отличается от предела 1 на б.м.в., т.е.
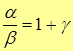 , где γ – б.м.в. (если
, где γ – б.м.в. (если  ).
).
Откуда 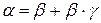 , но
, но 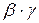 - б.м.в. более высокого порядка малости, чем
- б.м.в. более высокого порядка малости, чем 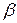 , т.е.
, т.е. 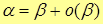 , ч.т.д.
, ч.т.д.
| Note 2 | Дома или на п/з аналогично доказать, что
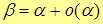 . .
|
| Def. | (Наизусть!) Дифференциалом функции y=f(x) в т. 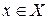 называют главную, линейную относительно приращения аргумента часть приращения функции, т.е. если называют главную, линейную относительно приращения аргумента часть приращения функции, т.е. если
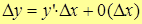 ,
то ,
то 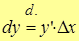 – дифференциал функции. – дифференциал функции.
|
| Note 3 | В математике принято приращение аргумента считать дифференциалом аргумента, т.е. 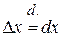 , тогда , тогда
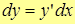 .
Откуда .
Откуда 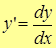 – читается «дэ игрек по дэ икс». – читается «дэ игрек по дэ икс».
|
| Note 4 | Следовательно, если 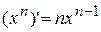 , то , то 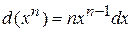 ;
если ;
если 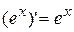 , то , то 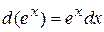 и т.д. и т.д.
|
| Note 5 | Дома или на п/з составить таблицу дифференциалов элементарных функций . |
Инвариантность формы записи дифференциала
1.Пусть x – основной аргумент функции y=f(x), 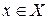 .
.
Тогда дифференциал 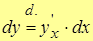 .
.
2.Пусть x – промежуточный аргумент сложной функции y=y[x(t)].
Тогда по определению дифференциала 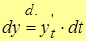 , или, учитывая формулу дифференцирования сложной функции
, или, учитывая формулу дифференцирования сложной функции 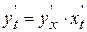 , получим
, получим
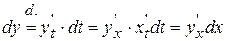 ,
,
т.е. формула записи для дифференциала не изменилась. Это свойство дифференциала называют инвариантностью:
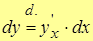 .
.
Дата добавления: 2015-08-20; просмотров: 1550;
