Теоремы о непрерывных функциях на отрезке
| Т.1. | (Первая теорема Больцано-Коши[10] ).
Пусть функция y=f(x) определена и непрерывна на отрезке [a;b].
Пусть 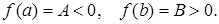 Тогда
Тогда 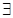 т. т. 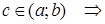 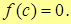
|

Т.о., если 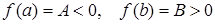 , то найдется такая точка
, то найдется такая точка 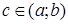 , в которой график функции y=f(x) пересекает ось 0X.
, в которой график функции y=f(x) пересекает ось 0X.
| Т.2. | (Вторая теорема Больцано-Коши).
Пусть функция y=f(x) определена и непрерывна на отрезке [a;b].
Пусть 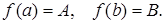 Пусть
Пусть 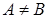 (например, A<B).
Тогда (например, A<B).
Тогда 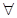 т. т. 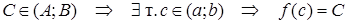 . .
|

Т.о., функция y=f(x) заполняет все значения от А до B сплошь.
| Т.3. | (Первая теорема Вейерштрасса[11]).
Пусть функция y=f(x) определена и непрерывна на отрезке [a;b], тогда она ограничена на нем, т.е. 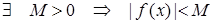 на [a;b]. на [a;b].
|
| Т.4. | (Вторая теорема Вейерштрасса).
Пусть функция y=f(x) определена и непрерывна на отрезке [a;b]. Тогда она достигает на этом отрезке точной верхней М и нижней m грани, т.е. . 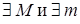 : :
 , ,  . .
|
| Т.5. | (Теорема Кантора[12]). Если функция непрерывна на отрезке, то она равномерно непрерывна на нем. |
Дата добавления: 2015-08-20; просмотров: 964;
