Непрерывность сложной функции
| Т. | Пусть функция u(x) – непрерывна в т. 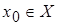 и ее окрестности.
Пусть при этих значениях u(x) функция y=y(u) тоже непрерывна. Тогда сложная функция y=y[u(x)] непрерывна в т. и ее окрестности.
Пусть при этих значениях u(x) функция y=y(u) тоже непрерывна. Тогда сложная функция y=y[u(x)] непрерывна в т. 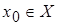 . .
|
Proоf:
Так как функция u(x) – непрерывна в т. x0, то 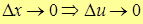 .
.
Т.к. функция y=y(u) – непрерывная при этих значениях u, то 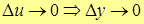 .
.
Таким образом, мы получили
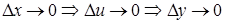
или
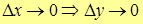 , ч.т.д.
, ч.т.д.
| Note | Можно доказать, что все элементарные функции непрерывны в своей области определения. Для непрерывных функций знак предела и функции можно менять местами, т.е.
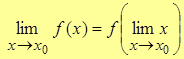 . .
|
Ex.1. 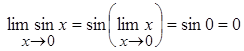 .
.
| Def. | Функция y=f(x) называется равномерно непрерывной на множестве X , если для любых 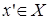 , , 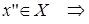
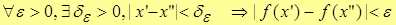 . .
|
Дата добавления: 2015-08-20; просмотров: 792;
