Разрывы. Классификация разрывов
| Def.1. | Функция y=f(x) называется разрывной в т. x0, если она не является непрерывной в этой точке. |
Пусть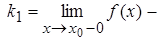 
левосторонний предел функции в т. x0,
правосторонний предел функции в т. x0.
| Def.2. | Функция y=f(x) имеет в т. x0 разрыв 1-го рода, если 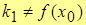 , или  , или  , причем, разность k2-k1=w – называют скачком функции в т. x0, если k1=k2, то разрыв называют устранимым.
|
| Def.3. | Функция y=f(x) имеет в т. x0 разрыв 2-го рода, если  , или  , или 
|
Ex.1. Исследовать функцию на непрерывность
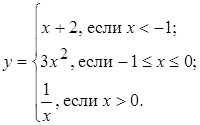
Т.к. все элементарные функции непрерывны в своей области определения, то остается исследовать в т. x=-1 и в т. x=0.
Построим схематически график этой функции.
1.Пусть x= -1.
Тогда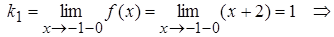 
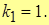
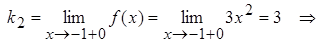
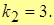
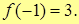
Т.к.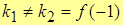 
, то в т. x = -1 разрыв 1-го рода. Причем, скачок функции w=k2 – k1 =3-1=2 => w=2.
2.Пусть x= 0.
Тогда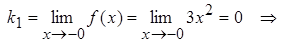 
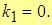
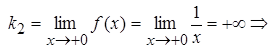
Т.к.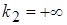 
, то в т. x = 0 разрыв 2-го рода.
Дата добавления: 2015-08-20; просмотров: 692;