Непрерывность функции. Непрерывность сложной функции. Равномерная непрерывность
Пусть функция y=f(x) определена в некоторой окрестности т. x0 множества X (и в самой точке x0 !!!).
| Def. 1 | Функция y=f(x) называется непрерывной в т. 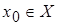 , если , если
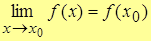
|
| Def. 2 | Функция y=f(x) называется непрерывной в т. 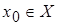 , если , если
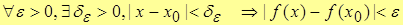 . .
|
| Def. 3 | Функция y=f(x) называется непрерывнойв т. 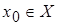 , если , если
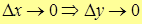 ,
где ,
где 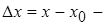 приращение аргумента; приращение аргумента;
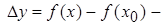 приращение функции;
т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. приращение функции;
т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
|
| Def. 4 | (Применяется при исследовании функции на непрерывность)
Функция y=f(x) называется непрерывной в т. 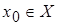 , если
1) она определена в т. x0 и ее окрестности;
2) , если
1) она определена в т. x0 и ее окрестности;
2) 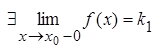 и и 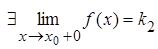 ;
3) k1 = k2 = f(x0). ;
3) k1 = k2 = f(x0).
|
Дата добавления: 2015-08-20; просмотров: 964;
