Бесконечные функциональные произведения, равномерная сходимость. Бесконечные произведения Бляшке
А. Произведение Бляшке
Если 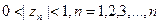 .., и бесконечное произведение
.., и бесконечное произведение

сходится для |z|< 1, то оно представляет некоторуюфункцию, аналитическую в единичном круге; она называется произведением Бляшке. Можно даже допустить равенство конечного числа чисел zn нулю - просто в этом случае множители, соответствующие 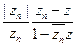 заменяются на z.
заменяются на z.
Имеем
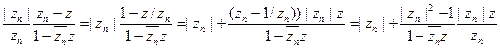
откуда
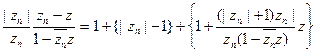
следовательно, рассматриваемое бесконечное произведение сходится при z = 0 тогда в только тогда, когда
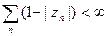
Но если 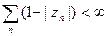 , то по той же только что найденной формуле
, то по той же только что найденной формуле
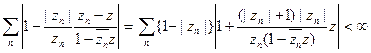
при |z|<1; поэтому бесконечное произведение сходится в {\z\ < 1}, если 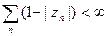 . Таким образом,
. Таким образом,
 сходится в {|z|<1} тогда и только тогда, когда
сходится в {|z|<1} тогда и только тогда, когда 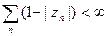 .
.
Дата добавления: 2015-08-14; просмотров: 1247;
