Ряд Тэйлора конформного отображении абсолютно сходится вплоть до границы

Теорема (Харди). Степенной ряд функции Ф(z) абсолютно сходится вплоть до {|z|= 1}.

Дoказательство.

По подпункту 1° имеем 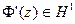. Кроме того, поскольку отображение Ф конформно, то Ф'(z) не обращается в нуль в {|z|<1}. Следовательно, мы можем определить аналитическую в {|z|<1} функцию 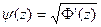Теперь, для |z|< 1 запишем

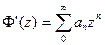
Тогда

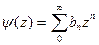
где

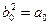
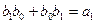
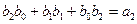
и т.д.

Так как 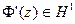, то средние

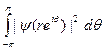
ограничены при r < 1. По равенству Парсеваля отсюда следует, что

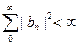
Теперь положим

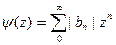
Используя равенство Парсеваля, получаем, что средние

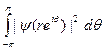
ограничены при r< 1.

Пусть θ(z) = [ψ(z)]² разлагается, скажем, в степенной ряд 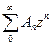Тогда, с одной стороны, 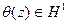, а с другой —

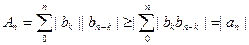
Имеем

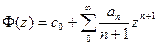
так что для доказательства абсолютной сходимости степен­ного ряда функции Ф(z) вплоть до {|z|= 1} нам надо показать, что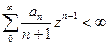

Для |z|< 1, взяв главную ветвь логарифма, получаем

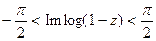
и

так что

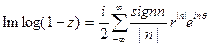
для z = rе^iθ, 0<r<1; умножая на 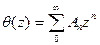и используя абсолютную сходимость и ортогональность находим что

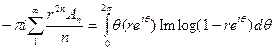
это по абсолютной величине не превосходит 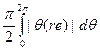, что равномерно по r< 1 ограничено, скажем, константой М. Поскольку А_n ≥ 0, то мы получаем, устремляя r к I, что

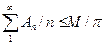, как и требовалось.