Образы множеств меры нуль на единичной окружности
Если А — дуга кривой Г, то Ф взаимно-однозначно отображает некоторую дугу j окружности {|z|=1} на Ʌ. Само определение длины дуги теперь нам дает
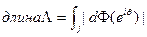
Теорема (Ф. и М.. Риссы). Если. j — дуга единичной окружности и 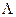 = Ф(j),то
= Ф(j),то
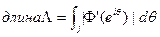
Доказательство.
По теореме предыдущего подпункта 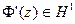 , поэтому
, поэтому
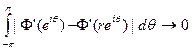 при r→1
при r→1
Пусть Т(θ) — непрерывно дифференцируемая 2π-периидичеекая функция. Интегрируя по частям, находим
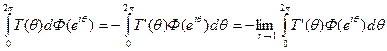
Но при любом r< 1
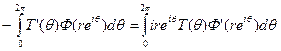
Правая часть этого равенства по замечанию, желанному вначале, стремится к 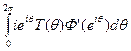 Итак,
Итак,
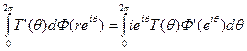
Б о
какова бы ни была 2π-периодическая непрерывно дифференцируемая функция Т. Пусть теперь 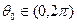 , а
, а 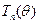 — равномерно ограниченная последовательность таких функций, сходящаяся к единице в (0,θ0) и к нулю в [0, 2π] \(0,θ0). Подставляя Тп вместо Т в последнее равенство и переходя к пределу, по теореме Лебега получаем
— равномерно ограниченная последовательность таких функций, сходящаяся к единице в (0,θ0) и к нулю в [0, 2π] \(0,θ0). Подставляя Тп вместо Т в последнее равенство и переходя к пределу, по теореме Лебега получаем

Следовательно,
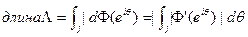
Теорема доказана,
Длина дуги кривой Г может быть очевидным образом использована для определения линейной меры на Г. Сначалапусть Ơ 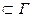 — (относительно) открытое подмножество Г тогда Ơ есть счётное объединение попарно Heпepeceкающихся открытых дуг Ʌk, и мы положим |Ơ|=
— (относительно) открытое подмножество Г тогда Ơ есть счётное объединение попарно Heпepeceкающихся открытых дуг Ʌk, и мы положим |Ơ|= 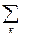 длина Ʌk. Для произвольного подмножества
длина Ʌk. Для произвольного подмножества 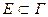 определим |E| какinf{|Ơ|: Ơ
определим |E| какinf{|Ơ|: Ơ  , Ơоткрыто в Г}. Так как Ф — гомеоморфное отображение окружности {|z|= 1} на Г, то легко показать, основываясь на вышеприведенной теореме, что
, Ơоткрыто в Г}. Так как Ф — гомеоморфное отображение окружности {|z|= 1} на Г, то легко показать, основываясь на вышеприведенной теореме, что 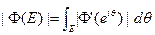
борелевсках множеств Е на единичной окружности. Имеет место следующий важный результат:
Теорема (Ф. и М. Риссы). Если Е - подмножество единичной окружности и {|z|= 1}, то |Ф(Е)| = 0.
Доказательство.
Пусть  — открытые множества на {|z|= 1},
— открытые множества на {|z|= 1}, 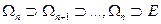 такие что
такие что 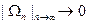 Тогда |Ф(Е)|≤|Ф(Ωп) | для всех n. Но из предыдущей теоремы н следующего за ней обсуждения вытекает, что
Тогда |Ф(Е)|≤|Ф(Ωп) | для всех n. Но из предыдущей теоремы н следующего за ней обсуждения вытекает, что
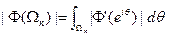
этот интеграл стремится к нулю при 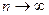 так как
так как 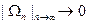 и
и 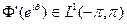 .
.
Дата добавления: 2015-08-14; просмотров: 685;
