Аналитической в единичном круге

Теорема. Пусть функция F(z) регулярна в круге {|z|<1} и z_п — её нули в этом круге, |z_n| < 1. Предположим, что интегралы

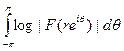
ограничены сверху при r< 1. Тогда

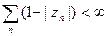
так что произведение

сходится в {|z|<1} и имеет место равенство F[z)=b(z) g(z), где функция g(z) регулярна и не имеет нулей в круге {|z|<1}

Доказательство.

Без ограничения общности можно счи­тать, что F(0)≠0; иначе мы рассмотрели бы функцию F(z)/z^k вместо F(z). Тогда если 0<r<1 и не существует точек z_n с |z_n|=r, то по формуле Йенсена

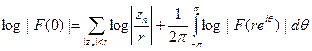
т, е., по предположению,

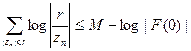
где М ие зависит от r. Устремляя r к I, получаем, что для любого фиксированного числа р

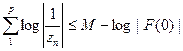
Следовательно,

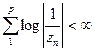
Существование произведения Бляшке b(z) доказано ранее. Наконец, определим функцию g(z) в круге {[r]< 1} но формуле g(z)= f(z)/b{z). Вот в всё.