Весовое пространство аналитических в круге функций
Пусть 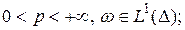 обозначим через
обозначим через  – класс всех аналитических в
– класс всех аналитических в  функций
функций 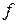 , для которых
, для которых
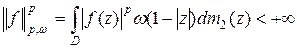 .
.
Если 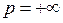 , мы отождествим
, мы отождествим 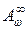 с классом ограниченных аналитических в круге функций
с классом ограниченных аналитических в круге функций 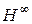 .
.
Нетрудно заметить, что условие 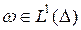 является необходимым условием для нетривиальности класса
является необходимым условием для нетривиальности класса  .
.
Если 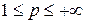 , то
, то  определяет норму на пространстве
определяет норму на пространстве  , а если
, а если 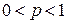 , то – квазинорму на пространстве
, то – квазинорму на пространстве 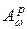 .
.
Непосредственно из неравенства Гёльдера следует, что 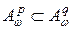 , если
, если 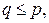 и
и 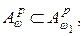 если
если 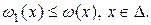
В дальнейшем, если не оговорено противное, будем предполагать, что 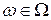 , причем
, причем 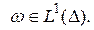
Следующее утверждение позволяет определить рост модуля функции из класса 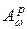 .
.
Теорема 1.Пусть 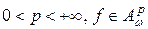 , тогда справедлива оценка
, тогда справедлива оценка
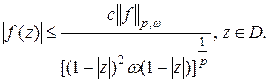 (1)
(1)
Доказательство. Пусть 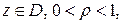
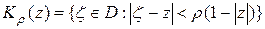 .
.
Очевидно, что 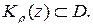 В силу субгармоничности функции
В силу субгармоничности функции 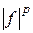 имеем:
имеем:
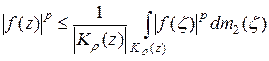 (2)
(2)
или
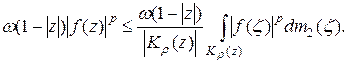
Теперь заметим, что 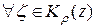 :
:
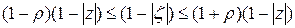 . (3)
. (3)
И
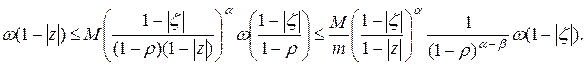
Напомним, что
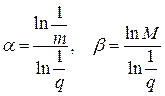 .
.
Положив 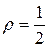 , из последнего неравенства выводим:
, из последнего неравенства выводим:
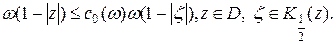
Учитывая неравенство (2.2), получаем:
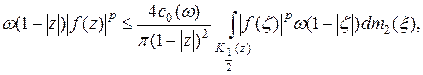
то есть
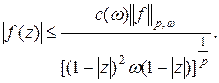 □
□
Следствие 1.Пусть 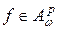 , тогда справедлива оценка
, тогда справедлива оценка
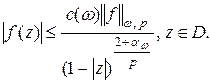 (4)
(4)
Доказательство непосредственно выводится из теоремы 1. □
При 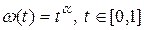 ,
, 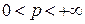 , для краткости обозначим
, для краткости обозначим 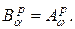
Следствие 2.Пусть 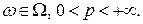 Тогда если
Тогда если 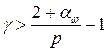 , то
, то
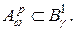
Доказательство. Действительно, если 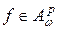 , то, используя оценку (4), непосредственно получаем:
, то, используя оценку (4), непосредственно получаем:
 □
□
Теорема 2.Пусть 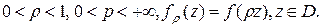 Тогда справедливо равенство
Тогда справедливо равенство
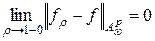 .
.
Доказательство очевидно, так как при всех 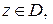
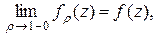
при этом
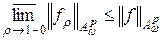 .
.
Докажем данную оценку. Имеем:
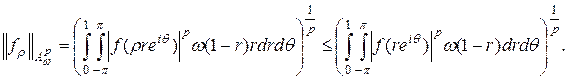
В последнем неравенстве мы использовали монотонность функции 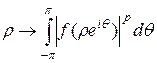 при
при 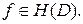 Учитывая полученную оценку, имеем:
Учитывая полученную оценку, имеем:
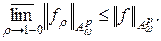
Поэтому из теоремы 1.7 непосредственно следует утверждение теоремы 2.2. □
2. Интегральное представление классов 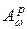
Важную роль в изучении классов 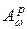 играет интегральное представление функций из этих классов.
играет интегральное представление функций из этих классов.
Сначала докажем следующее утверждение:
Теорема 3.Пусть 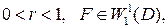 где
где 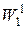 – класс Соболева в
– класс Соболева в  . Если при этом существует такое число
. Если при этом существует такое число 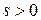 , что
, что 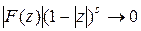 и
и 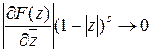 при
при 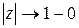 , то при всех
, то при всех 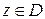 справедливо представление
справедливо представление
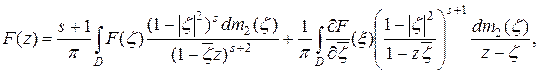 (2.5)
(2.5)
где, как обычно, 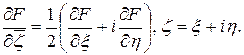
Доказательство. Пусть  фиксировано, положим
фиксировано, положим
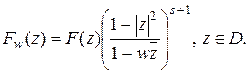 Тогда, записав формулу Коши-Грина для функции
Тогда, записав формулу Коши-Грина для функции 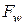 , имеем:
, имеем:
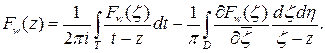
Используя условие теоремы, получаем:
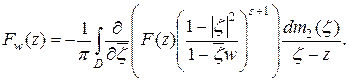
Упростим подынтегральное выражение:
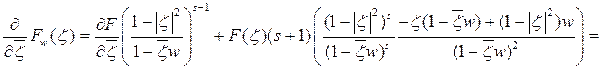

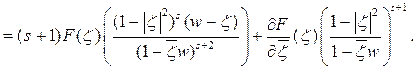
Следовательно, из равенства (5) имеем:
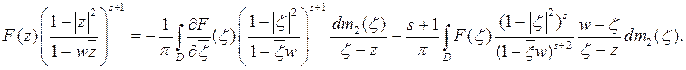
Положив  , получаем:
, получаем:
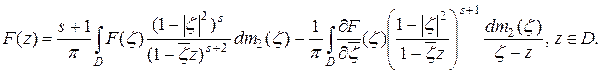 □
□
Из теоремы 3 непосредственно следует:
Теорема 4.Пусть 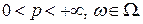 . Тогда если
. Тогда если 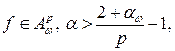 или
или 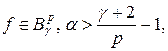 то справедливо представление
то справедливо представление
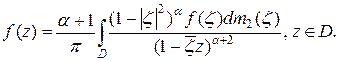 (6)
(6)
Доказательство непосредственно следует из теоремы 2.3, если учесть, что 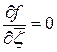 , при этом в условиях теоремы 2.4
, при этом в условиях теоремы 2.4 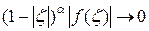 при
при 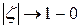 .
.
□
Из интегрального представления классов  вытекает:
вытекает:
Теорема 5. Пространство 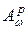 при
при 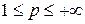 относительно нормы
относительно нормы
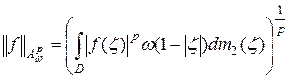
является банаховым, а при 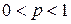 – квазибанаховым пространством.
– квазибанаховым пространством.
Доказательство. Пусть 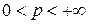 . Обозначим через
. Обозначим через 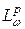 пространство измеримых в
пространство измеримых в 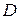 функций
функций 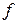 , для которых соответствующий интеграл конечен.
, для которых соответствующий интеграл конечен.
Хорошо известно, что пространство 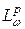 при
при 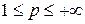 банахово, а при
банахово, а при 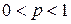 квазибанахово. Поэтому достаточно установить, что
квазибанахово. Поэтому достаточно установить, что 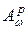 является замкнутым подпространством пространства
является замкнутым подпространством пространства 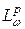 при всех
при всех 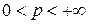 .
.
Предположим, что  – последовательность из
– последовательность из 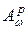 , а функция
, а функция 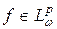 такая, что
такая, что 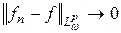 при
при 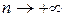 .
.
Докажем, что 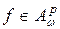 . Используя оценку (2.1), имеем:
. Используя оценку (2.1), имеем:
 .
.
Отсюда следует, что последовательность  равномерно сходится внутри
равномерно сходится внутри 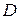 к некоторой функции
к некоторой функции  . Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательность
. Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательность 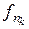 такую, что
такую, что 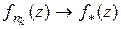 почти всюду в
почти всюду в 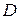 . Поэтому
. Поэтому 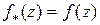 почти всюду в
почти всюду в 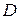 , и следовательно,
, и следовательно, 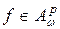 . □
. □
Дата добавления: 2015-08-14; просмотров: 915;
