Формула Коши
Теорема. Пусть D — область на комплексной плоскости с кусочно-гладкой границей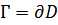 
, функция f(z) — голоморфна в 
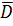и 
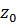— точка внутри области D. Тогда справедлива следующая формула Коши:
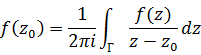
Док-во
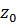. Г
Рассмотрим окружность Sρ достаточно малого радиуса ρ с центром в точке z0. В области, ограниченной контурами Γ и Sρ подынтегральная функция не имеет особенностей и по интегральной теореме Коши интеграл от неё по границе этой области равен нулю. Это означает, что не зависимо от ρ имеем равенство:
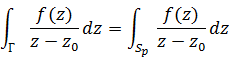
Для расчёта интегралов по Sρ применим параметризацию.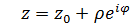 
, φ Є 
Сначала докажем формулу Коши отдельно для случая f(z) = 1:
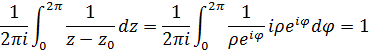
Воспользуемся ею для доказательства общего случая:
= 
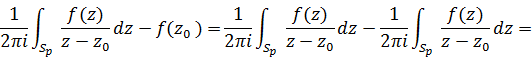
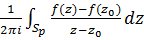
Так как функция f(z) комплексно дифференцируема в точке z0, то:
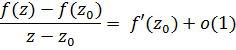
Интеграл от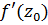 
равен нулю:
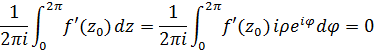
Интеграл от члена o(1) может быть сделан сколь угодно мал при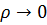 
. Но поскольку он от ρ вообще не зависит, значит он равен нулю. В итоге получаем, что
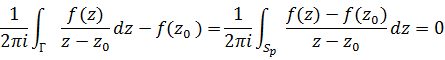
Дата добавления: 2015-08-14; просмотров: 705;